Advertisements
Advertisements
Question
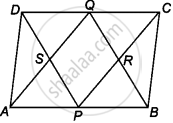
P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.
Solution
Given: In a parallelogram ABCD, P and Q are the mid-points of AS and CD, respectively.
To show: PRQS is a parallelogram.
Proof: Since, ABCD is a parallelogram.
AB || CD
⇒ AP || QC
Also, AB = DC
`1/2`AB = `1/2`DC ...[Dividing both sides by 2]
⇒ AP = QC ...[Since, P and Q are the mid-points of AB and DC]
Now, AP || QC and AP = QC
Thus, APCQ is a parallelogram.
∴ AQ || PC or SQ || PR ...(i)
Again, AB || DC or BP || DQ
Also, AB = DC
⇒ `1/2`AB = `1/2`DC ...[Dividing both sides by 2]
⇒ BP = QD ...[Since, P and Q are the mid-points of AB and DC]
Now, BP || QD and BP = QD
So, BPDQ is a parallelogram.
∴ PD || BQ or PS || QR ...(ii)
From equations (i) and (ii),
SQ || RP and PS || QR
So, PRQS is a parallelogram.
Hence proved.
APPEARS IN
RELATED QUESTIONS
In a ΔABC, BM and CN are perpendiculars from B and C respectively on any line passing
through A. If L is the mid-point of BC, prove that ML = NL.
In ∆ABC, E is the mid-point of the median AD, and BE produced meets side AC at point Q.
Show that BE: EQ = 3: 1.
In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
The side AC of a triangle ABC is produced to point E so that CE = AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively.
Prove that:
- 3DF = EF
- 4CR = AB
In triangle ABC, the medians BP and CQ are produced up to points M and N respectively such that BP = PM and CQ = QN. Prove that:
- M, A, and N are collinear.
- A is the mid-point of MN.
If L and M are the mid-points of AB, and DC respectively of parallelogram ABCD. Prove that segment DL and BM trisect diagonal AC.
AD is a median of side BC of ABC. E is the midpoint of AD. BE is joined and produced to meet AC at F. Prove that AF: AC = 1 : 3.
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
If AE and DF intersect at G, and M and N are the midpoints of GB and GC respectively, prove that DMNF is a parallelogram.
In AABC, D and E are two points on the side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet the side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meet the side BC at points M and N respectively. Prove that BM = MN = NC.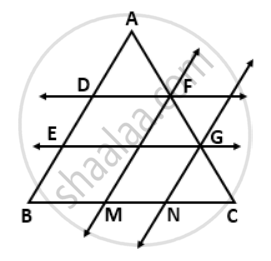
The figure obtained by joining the mid-points of the sides of a rhombus, taken in order, is ______.
