Advertisements
Advertisements
Question
AD is a median of side BC of ABC. E is the midpoint of AD. BE is joined and produced to meet AC at F. Prove that AF: AC = 1 : 3.
Solution
Construction: Draw DS ∥ BF, meeting AC at S.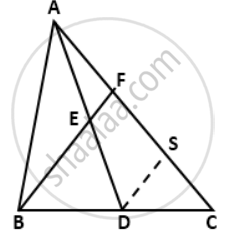
Proof:
In ΔBCF, D is the mid-point of AC DS || BF.
∴ S is the mid-point of CF.
⇒ CS = SF ....(i)
In ΔADS, E is the mid-point of AD and EF || DS.
∴ F is the mid-point of AS.
⇒ AF = FS ....(ii)
From (i) and (ii), we get
AF = FS = SC
⇒ AC = AF = FS + SC
⇒ AC = AF + AF +AF
⇒ AC = 3AF
⇒ `"AF"/"AC" = (1)/(3)`
⇒ AF : AC = 1 : 3.
APPEARS IN
RELATED QUESTIONS
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
The side AC of a triangle ABC is produced to point E so that CE = AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively.
Prove that:
- 3DF = EF
- 4CR = AB
In triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle,
show that the diagonals AC and BD intersect at the right angle.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: DC, if AB = 20 cm and PQ = 14 cm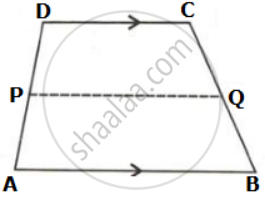
Side AC of a ABC is produced to point E so that CE = `(1)/(2)"AC"`. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meets AC at point P and EF at point R respectively. Prove that: 4CR = AB.
ΔABC is an isosceles triangle with AB = AC. D, E and F are the mid-points of BC, AB and AC respectively. Prove that the line segment AD is perpendicular to EF and is bisected by it.
ABCD is a parallelogram.E is the mid-point of CD and P is a point on AC such that PC = `(1)/(4)"AC"`. EP produced meets BC at F. Prove that: F is the mid-point of BC.
ABCD is a parallelogram.E is the mid-point of CD and P is a point on AC such that PC = `(1)/(4)"AC"`. EP produced meets BC at F. Prove that: 2EF = BD.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: EGFH is a parallelogram.
