Advertisements
Advertisements
Question
ABCD is a parallelogram.E is the mid-point of CD and P is a point on AC such that PC = `(1)/(4)"AC"`. EP produced meets BC at F. Prove that: F is the mid-point of BC.
Solution
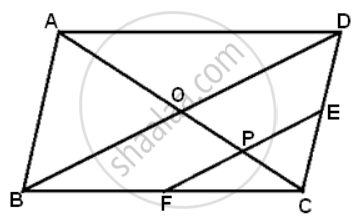
Join B and D. Suppose AC and BD cut at O. Then,
OC = `(1)/(2)"AC"`
Now,
PC = `(1)/(4)"AC"`
⇒ PC = `(1)/(2)"OC"`
In ΔDCO, E and P are the mid-points of DC and OC respectively.
∴ EP || DO
Also, in ΔCOB, P is the midpoint of OC and PF || DO || BD
Therefore, F is the mid-point of BC, F being EP produced.
APPEARS IN
RELATED QUESTIONS
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
ABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP = PH
BM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If
L is the mid-point of BC, prove that LM = LN.
In the given figure, `square`PQRS and `square`MNRL are rectangles. If point M is the midpoint of side PR then prove that,
- SL = LR
- LN = `1/2`SQ

In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
A parallelogram ABCD has P the mid-point of Dc and Q a point of Ac such that
CQ = `[1]/[4]`AC. PQ produced meets BC at R.

Prove that
(i)R is the midpoint of BC
(ii) PR = `[1]/[2]` DB
In ΔABC, D is the mid-point of AB and E is the mid-point of BC.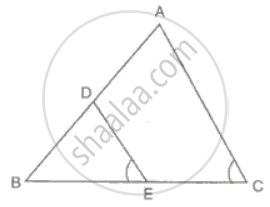
Calculate:
(i) DE, if AC = 8.6 cm
(ii) ∠DEB, if ∠ACB = 72°
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: ∠EFG = 90°
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: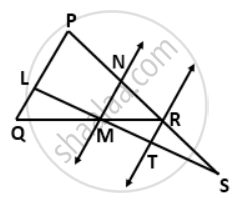
ST = `(1)/(3)"LS"`
