Advertisements
Advertisements
Question
A parallelogram ABCD has P the mid-point of Dc and Q a point of Ac such that
CQ = `[1]/[4]`AC. PQ produced meets BC at R.

Prove that
(i)R is the midpoint of BC
(ii) PR = `[1]/[2]` DB
Solution
For help, we draw the diagonal BD as shown below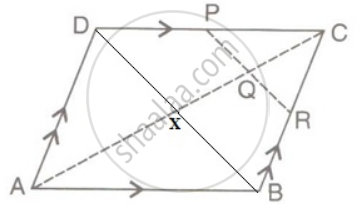
The diagonal AC and BD cuts at point X.
We know that the diagonal of a parallelogram intersect equally with each other. Therefore
AX = CX and BX = DX
Given,
CQ = `[1]/[4]`AC
CQ = `[1]/[4]` x 2CX
CQ = `[1]/[2]`CX
Therefore Q is the midpoint of CX.
(i) For triangle CDX PQ || DX or PR || BD
Since for triangle CBX
Q is the midpoint of CX and QR || BX. Therefore R is the midpoint of BC
(ii) For triangle BCD
As P and R are the mid-point of CD and BC, therefore PR = `[1]/[2]` DB
APPEARS IN
RELATED QUESTIONS
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
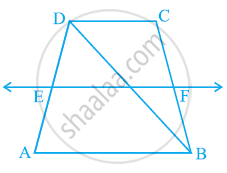
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
L and M are the mid-point of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
Use the following figure to find:
(i) BC, if AB = 7.2 cm.
(ii) GE, if FE = 4 cm.
(iii) AE, if BD = 4.1 cm
(iv) DF, if CG = 11 cm.
In parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The line segments AF and BF meet the line segments ED and EC at points G and H respectively.
Prove that:
(i) Triangles HEB and FHC are congruent;
(ii) GEHF is a parallelogram.
The diagonals of a quadrilateral intersect each other at right angle. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.
ΔABC is an isosceles triangle with AB = AC. D, E and F are the mid-points of BC, AB and AC respectively. Prove that the line segment AD is perpendicular to EF and is bisected by it.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if ______.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rhombus, if ______.
