Advertisements
Advertisements
प्रश्न
A parallelogram ABCD has P the mid-point of Dc and Q a point of Ac such that
CQ = `[1]/[4]`AC. PQ produced meets BC at R.

Prove that
(i)R is the midpoint of BC
(ii) PR = `[1]/[2]` DB
उत्तर
For help, we draw the diagonal BD as shown below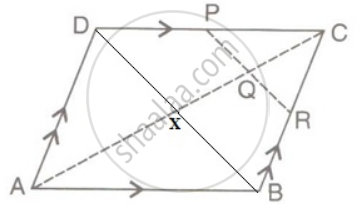
The diagonal AC and BD cuts at point X.
We know that the diagonal of a parallelogram intersect equally with each other. Therefore
AX = CX and BX = DX
Given,
CQ = `[1]/[4]`AC
CQ = `[1]/[4]` x 2CX
CQ = `[1]/[2]`CX
Therefore Q is the midpoint of CX.
(i) For triangle CDX PQ || DX or PR || BD
Since for triangle CBX
Q is the midpoint of CX and QR || BX. Therefore R is the midpoint of BC
(ii) For triangle BCD
As P and R are the mid-point of CD and BC, therefore PR = `[1]/[2]` DB
APPEARS IN
संबंधित प्रश्न
ABCD is a rhombus, EABF is a straight line such that EA = AB = BF. Prove that ED and FC when produced meet at right angles
In a ΔABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC
intersects FE at Q. Prove that AQ = QP.
In the given figure, `square`PQRS and `square`MNRL are rectangles. If point M is the midpoint of side PR then prove that,
- SL = LR
- LN = `1/2`SQ

In triangle ABC, M is mid-point of AB and a straight line through M and parallel to BC cuts AC in N. Find the lengths of AN and MN if Bc = 7 cm and Ac = 5 cm.
The figure, given below, shows a trapezium ABCD. M and N are the mid-point of the non-parallel sides AD and BC respectively. Find:

- MN, if AB = 11 cm and DC = 8 cm.
- AB, if DC = 20 cm and MN = 27 cm.
- DC, if MN = 15 cm and AB = 23 cm.
In trapezium ABCD, AB is parallel to DC; P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E.
Prove that:
- Point P bisects BE,
- PQ is parallel to AB.
In triangle ABC; M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use the intercept Theorem to show that MN bisects AD.
In ΔABC, D is the mid-point of AB and E is the mid-point of BC.
Calculate:
(i) DE, if AC = 8.6 cm
(ii) ∠DEB, if ∠ACB = 72°
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find DE, if AB = 8 cm
P, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC = BD and AC ⊥ BD. Prove that PQRS is a square.
