Advertisements
Advertisements
प्रश्न
In a ΔABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC
intersects FE at Q. Prove that AQ = QP.
उत्तर
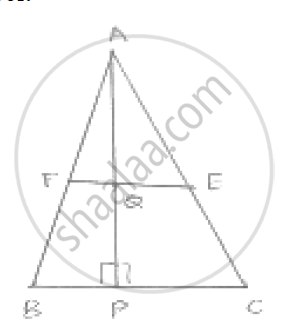
In ΔABC
E and F are midpoints of AB and AC
∴ EF || FE, `1/2` BC =FE [ ∴ By mid-point theorem]
In ΔABP
F is the midpoint of AB and FQ || BP [ ∵ EF || BC ]
∴ Q is the midpoint of AP [By converse of midpoint theorem]
Hence, AQ = QP
APPEARS IN
संबंधित प्रश्न
In Fig. below, triangle ABC is right-angled at B. Given that AB = 9 cm, AC = 15 cm and D,
E are the mid-points of the sides AB and AC respectively, calculate
(i) The length of BC (ii) The area of ΔADE.
The figure, given below, shows a trapezium ABCD. M and N are the mid-point of the non-parallel sides AD and BC respectively. Find:

- MN, if AB = 11 cm and DC = 8 cm.
- AB, if DC = 20 cm and MN = 27 cm.
- DC, if MN = 15 cm and AB = 23 cm.
The diagonals of a quadrilateral intersect at right angles. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is rectangle.
In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
In the given figure, AD and CE are medians and DF // CE.
Prove that: FB = `1/4` AB.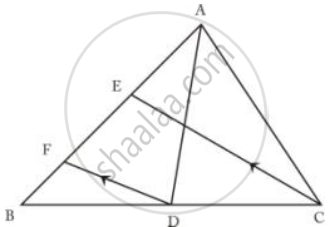
In ΔABC, X is the mid-point of AB, and Y is the mid-point of AC. BY and CX are produced and meet the straight line through A parallel to BC at P and Q respectively. Prove AP = AQ.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: ΔHEB ≅ ΔHFC
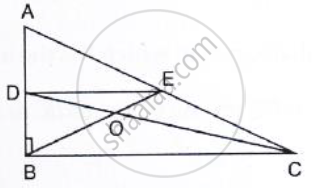
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: Q A and P are collinear.
P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD such that AC ⊥ BD. Prove that PQRS is a rectangle.
E is the mid-point of a median AD of ∆ABC and BE is produced to meet AC at F. Show that AF = `1/3` AC.
