Advertisements
Advertisements
प्रश्न
E is the mid-point of a median AD of ∆ABC and BE is produced to meet AC at F. Show that AF = `1/3` AC.
उत्तर
Given: In a ∆ABC, AD is a median and E is the mid-point of AD.
Construction: Draw DP || EF.
Proof: In ∆ADP, E is the mid-point of AD and EF || DP.
So, F is mid-point of AP. ...[By converse of mid-point theorem]
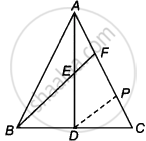
In ∆FBC, D is mid-point of BC and DP || BF.
So, P is mid-point of FC
Thus, AF = FP = PC
∴ AF = `1/3` AC
Hence proved.
APPEARS IN
संबंधित प्रश्न
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
In a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC =
21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ.
In a ΔABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC
intersects FE at Q. Prove that AQ = QP.
Let Abc Be an Isosceles Triangle in Which Ab = Ac. If D, E, F Be the Mid-points of the Sides Bc, Ca and a B Respectively, Show that the Segment Ad and Ef Bisect Each Other at Right Angles.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
A parallelogram ABCD has P the mid-point of Dc and Q a point of Ac such that
CQ = `[1]/[4]`AC. PQ produced meets BC at R.

Prove that
(i)R is the midpoint of BC
(ii) PR = `[1]/[2]` DB
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square is also a square.
In ΔABC, D and E are the midpoints of the sides AB and AC respectively. F is any point on the side BC. If DE intersects AF at P show that DP = PE.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rhombus, if ______.
In ∆ABC, AB = 5 cm, BC = 8 cm and CA = 7 cm. If D and E are respectively the mid-points of AB and BC, determine the length of DE.
