Advertisements
Advertisements
प्रश्न
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square is also a square.
उत्तर
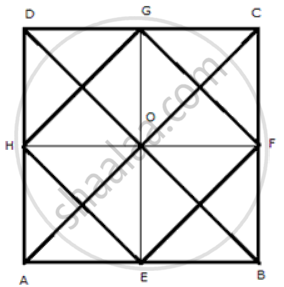
Join AC and BD
In ΔACD, G and H are the mid-points of DC and AC respectively.
Therefore, GH || AC and GH = `(1)/(2)"AC"` ......(i)
In ΔABC, E and F are the mid-points of AB and BC respectively.
Therefore, EF || AC and EF = `(1)/(2)"AC"` ......(i)
From (i) and (ii)
EF || GH and EF = GH = `(1)/(2)"AC"` .........(iii)
Similarly, it can be proved that
EF || GH and EH = GF = `(1)/(2)"BD"` .........(iv)
But AC = BD ...(diagonals of a square are equal)
Dividing both sides by 2,
`(1)/(2)"BD" = (1)/(2)"AC"` (iv)
From (iii) and (iv)
EF = Gh = EH = GF
Therefore, EFGH is a parallelogram.
Now in ΔGOH and ΔGOF
OH = OF ...(diagonals of a parallelogram bisect each other)
OG = O ...(common)
GH = GF
∴ ΔGOH ≅ ΔGOF
∴ ∠GOH = ∠GOF
Now,
∠GOH +∠GOF = 180°
⇒ ∠GOH + ∠GOH = 180°
⇒ 2∠GOH = 180°
⇒ ∠GOH = 90°
Therefore, diagonals of parallelogram EFGH bisect each other and are perpendicular to each other.
Thus, EFGH is a square.
APPEARS IN
संबंधित प्रश्न
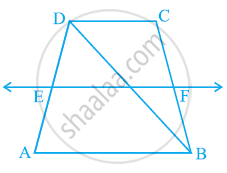
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
BM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If
L is the mid-point of BC, prove that LM = LN.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
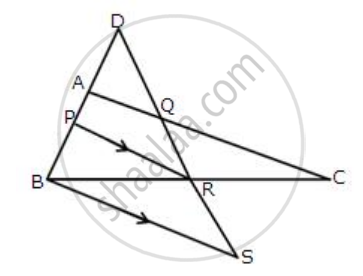
In the figure, give below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that:
(i) AQ // BS
(ii) DS = 3 Rs.
In triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meets side BC at points M and N respectively. Prove that: BM = MN = NC.
The diagonals of a quadrilateral intersect each other at right angle. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: EGFH is a parallelogram.
In ΔABC, D and E are the midpoints of the sides AB and AC respectively. F is any point on the side BC. If DE intersects AF at P show that DP = PE.
P, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC = BD and AC ⊥ BD. Prove that PQRS is a square.
P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.
