Advertisements
Advertisements
प्रश्न
In triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meets side BC at points M and N respectively. Prove that: BM = MN = NC.
उत्तर
The figure is shown below
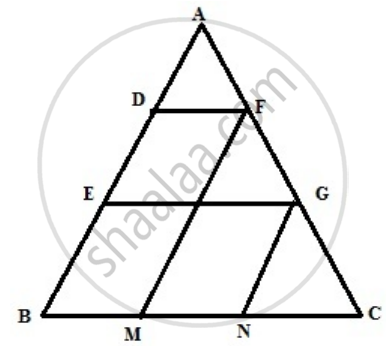
AD = DE = EB
In ΔAEG
AD = DE & DF || EG
Using mid point theorem
F is midpoint of AG
∴ AF = FG ...(1)
DF || EG || BC and DE = BE,
∴ FG = GC ...(2)
(1), (2) we get
AF = GF = GC
Similarly since GN || FM || AB
∴ BM = MN = NC
Hence, proved.
APPEARS IN
संबंधित प्रश्न
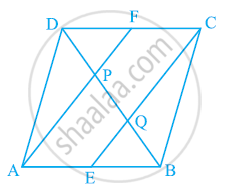
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see the given figure). Show that the line segments AF and EC trisect the diagonal BD.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
ABCD is a rhombus, EABF is a straight line such that EA = AB = BF. Prove that ED and FC when produced meet at right angles
ABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively
intersecting at P, Q and R. Prove that the perimeter of ΔPQR is double the perimeter of
ΔABC
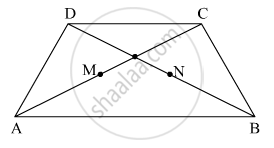
In the adjacent figure, `square`ABCD is a trapezium AB || DC. Points M and N are midpoints of diagonal AC and DB respectively then prove that MN || AB.
In triangle ABC, M is mid-point of AB and a straight line through M and parallel to BC cuts AC in N. Find the lengths of AN and MN if Bc = 7 cm and Ac = 5 cm.
D, E, and F are the mid-points of the sides AB, BC, and CA respectively of ΔABC. AE meets DF at O. P and Q are the mid-points of OB and OC respectively. Prove that DPQF is a parallelogram.
The side AC of a triangle ABC is produced to point E so that CE = AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively.
Prove that:
- 3DF = EF
- 4CR = AB
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P.
Prove that:
(i) BP = 2AD
(ii) O is the mid-point of AP.
E is the mid-point of the side AD of the trapezium ABCD with AB || DC. A line through E drawn parallel to AB intersect BC at F. Show that F is the mid-point of BC. [Hint: Join AC]
