Advertisements
Advertisements
प्रश्न
The side AC of a triangle ABC is produced to point E so that CE = AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively.
Prove that:
- 3DF = EF
- 4CR = AB
उत्तर
Consider the figure :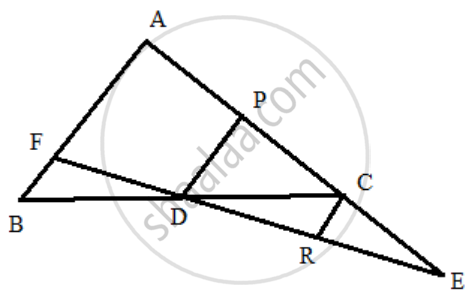
Here D is the midpoint of BC and DP is parallel to AB, therefore P is the midpoint of AC and
PD = `[1]/[2]`AB
(i) Again from the triangle AEF, we have AF || PD || CR and AP = `[1]/[3]`AE
Therefore, DF = `[1]/[3]` EF or we can say that 3DF = EF.
Hence, it is shown.
(ii) From the triangle PED, we have PD || CR and C is the midpoint of PE, therefore, CR = `[1]/[2]`PD
Now,
PD = `1/2` AB
`1/2"PD" = 1/4`AB
CR = `1/4`AB
4CR = AB
Hence, it is shown.
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
In Fig. below, triangle ABC is right-angled at B. Given that AB = 9 cm, AC = 15 cm and D,
E are the mid-points of the sides AB and AC respectively, calculate
(i) The length of BC (ii) The area of ΔADE.
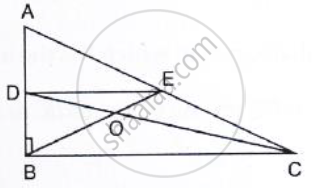
ABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP = PH
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral
bisect each other.
In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
A parallelogram ABCD has P the mid-point of Dc and Q a point of Ac such that
CQ = `[1]/[4]`AC. PQ produced meets BC at R.

Prove that
(i)R is the midpoint of BC
(ii) PR = `[1]/[2]` DB
In the given figure, AD and CE are medians and DF // CE.
Prove that: FB = `1/4` AB.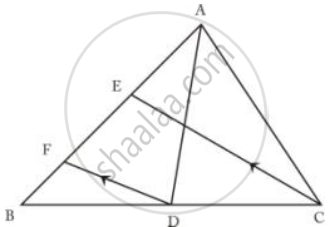
If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle,
show that the diagonals AC and BD intersect at the right angle.
In a parallelogram ABCD, M is the mid-point AC. X and Y are the points on AB and DC respectively such that AX = CY. Prove that:
(i) Triangle AXM is congruent to triangle CYM, and
(ii) XMY is a straight line.
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: Q A and P are collinear.
