Advertisements
Advertisements
प्रश्न
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
उत्तर
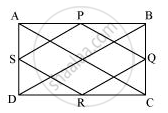
Let us join AC and BD.
In ΔABC,
P and Q are the mid-points of AB and BC respectively.
∴ PQ || AC and PQ = `1/2 AC` ...(Mid-point theorem) ...(1)
Similarly, in ΔADC,
SR || AC and SR = `1/2 AC` ...(Mid-point theorem) ...(2)
Clearly, PQ || SR and PQ = SR
Since in quadrilateral PQRS, one pair of opposite sides is equal and parallel to each other, it is a parallelogram.
∴ PS || QR and PS = QR ...(Opposite sides of the parallelogram) ...(3)
In ΔBCD, Q and R are the mid-points of side BC and CD respectively.
∴ QR || BD and QR = `1/2 BD` ...(Mid-point theorem) ...(4)
However, the diagonals of a rectangle are equal.
∴ AC = BD …(5)
By using equation (1), (2), (3), (4), and (5), we obtain
PQ = QR = SR = PS
Therefore, PQRS is a rhombus.
APPEARS IN
संबंधित प्रश्न
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
In a ΔABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC
intersects FE at Q. Prove that AQ = QP.
Let Abc Be an Isosceles Triangle in Which Ab = Ac. If D, E, F Be the Mid-points of the Sides Bc, Ca and a B Respectively, Show that the Segment Ad and Ef Bisect Each Other at Right Angles.
ABC is a triang D is a point on AB such that AD = `1/4` AB and E is a point on AC such that AE = `1/4` AC. Prove that DE = `1/4` BC.
In the below Fig, ABCD and PQRC are rectangles and Q is the mid-point of Prove thaT
i) DP = PC (ii) PR = `1/2` AC
In triangle ABC, the medians BP and CQ are produced up to points M and N respectively such that BP = PM and CQ = QN. Prove that:
- M, A, and N are collinear.
- A is the mid-point of MN.
In triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meets side BC at points M and N respectively. Prove that: BM = MN = NC.
D, E and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC. Prove that ΔDEF is also isosceles.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: EGFH is a parallelogram.
In ∆ABC, AB = 5 cm, BC = 8 cm and CA = 7 cm. If D and E are respectively the mid-points of AB and BC, determine the length of DE.
