Advertisements
Advertisements
प्रश्न
In triangle ABC, the medians BP and CQ are produced up to points M and N respectively such that BP = PM and CQ = QN. Prove that:
- M, A, and N are collinear.
- A is the mid-point of MN.
उत्तर
The figure is shown below
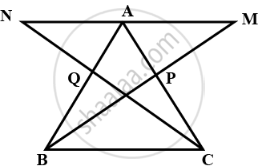
(i) In ΔAQN & ΔBQC
AQ = QB (Given)
∠AQN = ∠BQC
QN = QC
∴ ΔAQN ≅ ΔBQC ...[ by SAS ]
∴ ∠QAN = ∠QBC ...(1)
And BC = AN ……(2)
Similarly, ΔAPM ≅ ΔCPB .....[by SAS]
∠PAM = ∠PCB ...(3) [by CPTC]
And BC = AM ….( 4 )
Now In ΔABC,
∠ABC + ∠ACB + ∠BAC = 180°
∠QAN + ∠PAM + ∠BAC = 180° ...[ (1), (2) we get ]
Therefore M, A, N are collinear.
(ii) From (3) and (4) MA = NA
Hence A is the midpoint of MN.
APPEARS IN
संबंधित प्रश्न
In a ∆ABC, D, E and F are, respectively, the mid-points of BC, CA and AB. If the lengths of side AB, BC and CA are 7 cm, 8 cm and 9 cm, respectively, find the perimeter of ∆DEF.
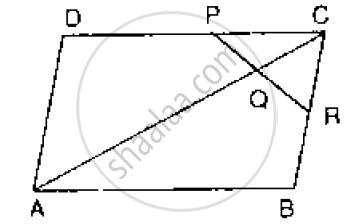
In below Fig, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.
In the given figure, seg PD is a median of ΔPQR. Point T is the mid point of seg PD. Produced QT intersects PR at M. Show that `"PM"/"PR" = 1/3`.
[Hint: DN || QM]

In the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF.
Show that: EF = AC.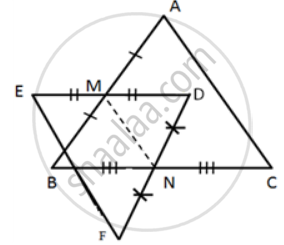
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P.
Prove that:
(i) BP = 2AD
(ii) O is the mid-point of AP.
In ΔABC, D is the mid-point of AB and E is the mid-point of BC.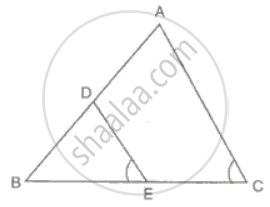
Calculate:
(i) DE, if AC = 8.6 cm
(ii) ∠DEB, if ∠ACB = 72°
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square is also a square.
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
Show that AE and DF bisect each other.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: EGFH is a parallelogram.
E is the mid-point of the side AD of the trapezium ABCD with AB || DC. A line through E drawn parallel to AB intersect BC at F. Show that F is the mid-point of BC. [Hint: Join AC]
