Advertisements
Advertisements
प्रश्न
E is the mid-point of the side AD of the trapezium ABCD with AB || DC. A line through E drawn parallel to AB intersect BC at F. Show that F is the mid-point of BC. [Hint: Join AC]
उत्तर
Given: E is the mid-point of the side AD of the trapezium ABCD with AB || DC.
Also, EF || AB.
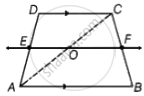
To prove: That F is the mid-point of BC.
Construction: Join AC which intersect EF at O.
Proof: In triangle ADC, E is the mid-point of AD and EF || DC. ...[Since, EF || AB and DC || AB. So, AB || EF || DC]
O is the mid-point of AC and OF || AB.
Now, OF bisect BC. ...[Converse of mid-point theorem]
Or F is the mid-point of BC.
Hence proved.
APPEARS IN
संबंधित प्रश्न
In a ∆ABC, D, E and F are, respectively, the mid-points of BC, CA and AB. If the lengths of side AB, BC and CA are 7 cm, 8 cm and 9 cm, respectively, find the perimeter of ∆DEF.
In a ΔABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC
intersects FE at Q. Prove that AQ = QP.
ABC is a triang D is a point on AB such that AD = `1/4` AB and E is a point on AC such that AE = `1/4` AC. Prove that DE = `1/4` BC.
In the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF.
Show that: EF = AC.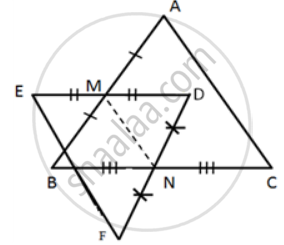
In triangle ABC, the medians BP and CQ are produced up to points M and N respectively such that BP = PM and CQ = QN. Prove that:
- M, A, and N are collinear.
- A is the mid-point of MN.
In trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that: AB + DC = 2EF.
In triangle ABC; M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use the intercept Theorem to show that MN bisects AD.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: AB, if DC = 8 cm and PQ = 9.5 cm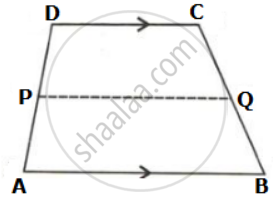
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
If AE and DF intersect at G, and M and N are the midpoints of GB and GC respectively, prove that DMNF is a parallelogram.
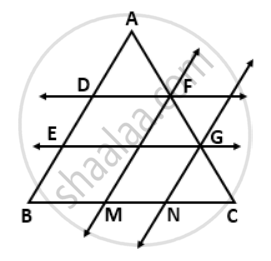
In AABC, D and E are two points on the side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet the side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meet the side BC at points M and N respectively. Prove that BM = MN = NC.