Advertisements
Advertisements
प्रश्न
In trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that: AB + DC = 2EF.
उत्तर
Consider trapezium ABCD.
Given E and F are midpoints on sides AD and BC, respectively.
We know that AB = GH = IJ
From midpoint theorem,
EG = `1/2"DI", "HF" = 1/2`JC
Consider LHS,
AB + CD = AB + CJ + JI + ID = AB + 2HF + AB + 2EG
So, AB + CD = 2( AB + HF + EG ) = 2( EG + GH + HF ) = 2EF
AB + CD = 2EF
Hence Proved.
APPEARS IN
संबंधित प्रश्न
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
In a ΔABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC
intersects FE at Q. Prove that AQ = QP.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral
bisect each other.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
In the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF.
Show that: EF = AC.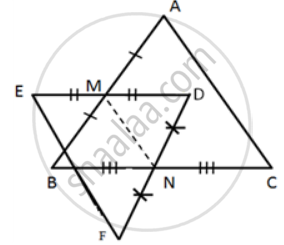
In ΔABC, BE and CF are medians. P is a point on BE produced such that BE = EP and Q is a point on CF produced such that CF = FQ. Prove that: A is the mid-point of PQ.
If L and M are the mid-points of AB, and DC respectively of parallelogram ABCD. Prove that segment DL and BM trisect diagonal AC.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: DC, if AB = 20 cm and PQ = 14 cm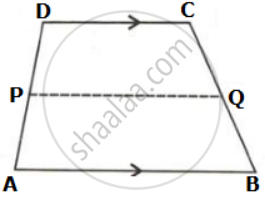
ABCD is a parallelogram.E is the mid-point of CD and P is a point on AC such that PC = `(1)/(4)"AC"`. EP produced meets BC at F. Prove that: F is the mid-point of BC.
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: A is the mid-point of PQ.
