Advertisements
Advertisements
Question
In trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that: AB + DC = 2EF.
Solution
Consider trapezium ABCD.
Given E and F are midpoints on sides AD and BC, respectively.
We know that AB = GH = IJ
From midpoint theorem,
EG = `1/2"DI", "HF" = 1/2`JC
Consider LHS,
AB + CD = AB + CJ + JI + ID = AB + 2HF + AB + 2EG
So, AB + CD = 2( AB + HF + EG ) = 2( EG + GH + HF ) = 2EF
AB + CD = 2EF
Hence Proved.
APPEARS IN
RELATED QUESTIONS
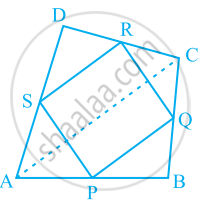
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see the given figure). AC is a diagonal. Show that:
- SR || AC and SR = `1/2AC`
- PQ = SR
- PQRS is a parallelogram.
D, E, and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC.
Prove that ΔDEF is also isosceles.
In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
D and F are midpoints of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
- Prove that BDFE is a parallelogram
- Find AB, if EF = 4.8 cm.
In trapezium ABCD, AB is parallel to DC; P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E.
Prove that:
- Point P bisects BE,
- PQ is parallel to AB.
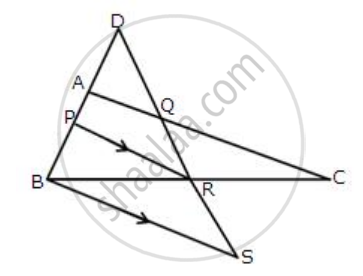
In the figure, give below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that:
(i) AQ // BS
(ii) DS = 3 Rs.
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: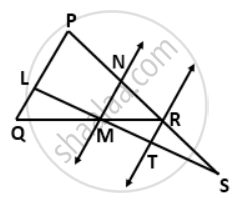
ST = `(1)/(3)"LS"`
The figure obtained by joining the mid-points of the sides of a rhombus, taken in order, is ______.
The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only if, ______.
E is the mid-point of a median AD of ∆ABC and BE is produced to meet AC at F. Show that AF = `1/3` AC.
