Advertisements
Advertisements
Question
The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only if, ______.
Options
ABCD is a rhombus
diagonals of ABCD are equal
diagonals of ABCD are equal and perpendicular
diagonals of ABCD are perpendicular
Solution
The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only if, diagonals of ABCD are equal and perpendicular.
Explanation:
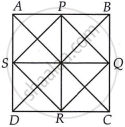
Given, ABCD is a quadrilateral and P, Q, R and S are the mid-points of sides of AB, BC, CD and DA, respectively.
Then, PQRS is a square.
∴ PQ = QR = RS = PS ...(i)
And PR = SQ
But PR = BC and SQ = AB
∴ AB = BC
Thus, all the sides of quadrilateral ABCD are equal.
Hence, quadrilateral ABCD is either a square or a rhombus.
Now, in ΔADB, use mid-point theorem
SP || DB
And SP = `1/2` DB ...(ii)
Similarly in ΔABC ...(By mid-point theorem)
PQ || AC and PQ = `1/2` AC ...(iii)
From equation (i),
PS = PQ
⇒ `1/2` DB = `1/2` AC ...[From equations (ii) and (iii)]
⇒ DB = AC
Thus, diagonals of ABCD are equal and therefore quadrilateral ABCD is a square not rhombus. So, diagonals of quadrilateral are also perpendicular.
APPEARS IN
RELATED QUESTIONS
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
- D is the mid-point of AC
- MD ⊥ AC
- CM = MA = `1/2AB`
In the given figure, seg PD is a median of ΔPQR. Point T is the mid point of seg PD. Produced QT intersects PR at M. Show that `"PM"/"PR" = 1/3`.
[Hint: DN || QM]

In ∆ABC, E is the mid-point of the median AD, and BE produced meets side AC at point Q.
Show that BE: EQ = 3: 1.
In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
In ΔABC, D is the mid-point of AB and E is the mid-point of BC.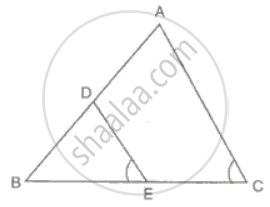
Calculate:
(i) DE, if AC = 8.6 cm
(ii) ∠DEB, if ∠ACB = 72°
If L and M are the mid-points of AB, and DC respectively of parallelogram ABCD. Prove that segment DL and BM trisect diagonal AC.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: DC, if AB = 20 cm and PQ = 14 cm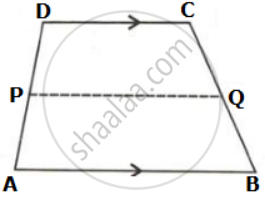
In ∆ABC, AB = 5 cm, BC = 8 cm and CA = 7 cm. If D and E are respectively the mid-points of AB and BC, determine the length of DE.
P, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC = BD and AC ⊥ BD. Prove that PQRS is a square.
Prove that the line joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides of the trapezium.
