Advertisements
Advertisements
Question
If L and M are the mid-points of AB, and DC respectively of parallelogram ABCD. Prove that segment DL and BM trisect diagonal AC.
Solution

Since L and M are the mid-points of AB and Dc respectively.
`"BL" = (1)/(2)"AB" and "Dm" = (1)/(2)"DC"`....(i)
But ABCD is a parallelogram
Therefore, AB = CD and AB || DC
⇒ BL = DM and BL || Dm ...(from (i))
⇒ BLDM is a parallelogram.
⇒ DL || Dm
⇒ LP || BQ ............(ii)
It is known that the segment drawn through the mid-point of one side of a triangle and parallel to the other side bisects the third side.
In ΔABQ , L is the mid-point of AB and MQ || PD
Therefore, P is mid-point of AQ
Hence, AP = PQ ..........(iii)
Similarly, in ΔCPD, M is the mid-point of CD and LP || BQ
Therefore, Q is mid-point of CP
Hence, PQ = QC ..........(iv)
From (iii) and (iv)
AP = PQ = QC
Therefore, P and Q trisect AC
Thus, DL and BM trisect AC.
APPEARS IN
RELATED QUESTIONS
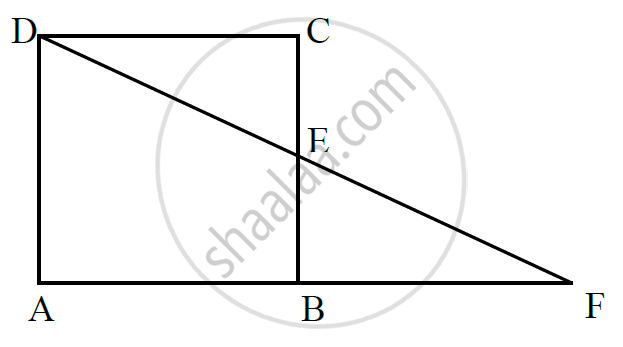
In below fig. ABCD is a parallelogram and E is the mid-point of side B If DE and AB when produced meet at F, prove that AF = 2AB.
Fill in the blank to make the following statement correct:
The triangle formed by joining the mid-points of the sides of a right triangle is
In the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF.
Show that: EF = AC.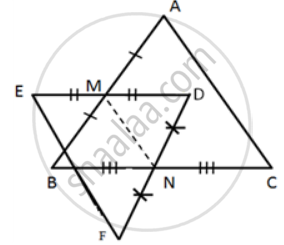
The figure, given below, shows a trapezium ABCD. M and N are the mid-point of the non-parallel sides AD and BC respectively. Find:

- MN, if AB = 11 cm and DC = 8 cm.
- AB, if DC = 20 cm and MN = 27 cm.
- DC, if MN = 15 cm and AB = 23 cm.
In trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that: AB + DC = 2EF.
D, E and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC. Prove that ΔDEF is also isosceles.
In a right-angled triangle ABC. ∠ABC = 90° and D is the midpoint of AC. Prove that BD = `(1)/(2)"AC"`.
In ΔABC, P is the mid-point of BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that: AP = 2AR
In ΔABC, X is the mid-point of AB, and Y is the mid-point of AC. BY and CX are produced and meet the straight line through A parallel to BC at P and Q respectively. Prove AP = AQ.
D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral triangle ABC. Show that ∆DEF is also an equilateral triangle.
