Advertisements
Advertisements
Question
Fill in the blank to make the following statement correct:
The triangle formed by joining the mid-points of the sides of a right triangle is
Solution
Right triangle
APPEARS IN
RELATED QUESTIONS
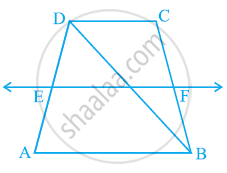
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
In a triangle ABC, AD is a median and E is mid-point of median AD. A line through B and E meets AC at point F.
Prove that: AC = 3AF.
In Δ ABC, AD is the median and DE is parallel to BA, where E is a point in AC. Prove that BE is also a median.
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find DE, if AB = 8 cm
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find ∠FDB if ∠ACB = 115°.
In ΔABC, X is the mid-point of AB, and Y is the mid-point of AC. BY and CX are produced and meet the straight line through A parallel to BC at P and Q respectively. Prove AP = AQ.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: EGFH is a parallelogram.
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: A is the mid-point of PQ.
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: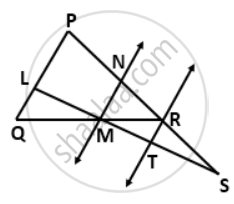
RT = `(1)/(3)"PQ"`
The figure obtained by joining the mid-points of the sides of a rhombus, taken in order, is ______.
