Advertisements
Advertisements
Question
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find DE, if AB = 8 cm
Solution
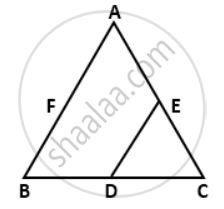
D is the mid-point BC and E is the mid-point of AC.
∴ DE = `(1)/(2)"AB"` ....(Mid-point Theorem)
= `(1)/(2) xx 8`
= 4 cm.
APPEARS IN
RELATED QUESTIONS
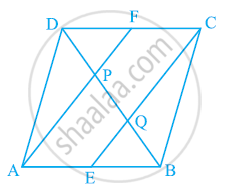
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see the given figure). Show that the line segments AF and EC trisect the diagonal BD.
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
- D is the mid-point of AC
- MD ⊥ AC
- CM = MA = `1/2AB`
ABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE = BF = CG = DH. Prove that EFGH is a square.
ABCD is a rhombus, EABF is a straight line such that EA = AB = BF. Prove that ED and FC when produced meet at right angles
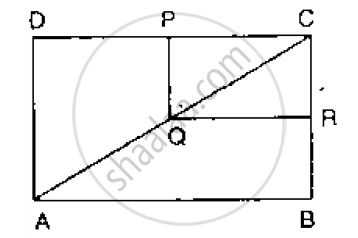
In the below Fig, ABCD and PQRC are rectangles and Q is the mid-point of Prove thaT
i) DP = PC (ii) PR = `1/2` AC
In the given figure, `square`PQRS and `square`MNRL are rectangles. If point M is the midpoint of side PR then prove that,
- SL = LR
- LN = `1/2`SQ

In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find FE, if BC = 14 cm
In AABC, D and E are two points on the side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet the side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meet the side BC at points M and N respectively. Prove that BM = MN = NC.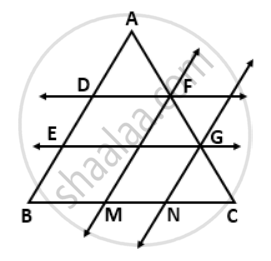
The diagonals AC and BD of a quadrilateral ABCD intersect at right angles. Prove that the quadrilateral formed by joining the midpoints of quadrilateral ABCD is a rectangle.
The figure obtained by joining the mid-points of the sides of a rhombus, taken in order, is ______.
