Advertisements
Advertisements
Question
The figure obtained by joining the mid-points of the sides of a rhombus, taken in order, is ______.
Options
a rhombus
a rectangle
a square
any parallelogram
Solution
The figure obtained by joining the mid-points of the sides of a rhombus, taken in order, is a rectangle.
Explanation:
The Midpoint Theorem states that the segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side.

Join AC, RP and SQ
In ∆ABC,
P is midpoint of AB and Q is midpoint of BC
∴ By midpoint theorem,
PQ || AC and PQ = `1/2` AC ...(1)
Similarly,
In ∆DAC,
S is midpoint of AD and R is midpoint of CD
∴ By midpoint theorem,
SR || AC and SR = `1/2` AC ...(2)
From (1) and (2),
PQ || SR and PQ = SR
⇒ PQRS is a parallelogram
ABQS is a parallelogram
⇒ AB = SQ
PBCR is a parallelogram
⇒ BC = PR
⇒ AB = PR ...[∵ BC = AB, sides of rhombus]
⇒ SQ = PR
∴ Diagonals of the parallelogram are equal.
Hence, it is a rectangle.
APPEARS IN
RELATED QUESTIONS
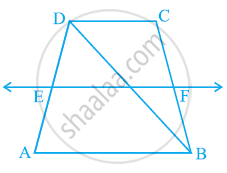
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
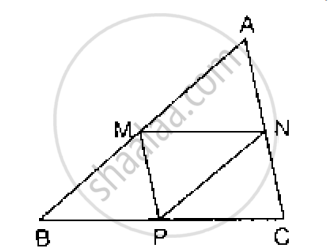
In a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC =
21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ.
In a ΔABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC
intersects FE at Q. Prove that AQ = QP.
In Fig. below, M, N and P are the mid-points of AB, AC and BC respectively. If MN = 3 cm, NP = 3.5 cm and MP = 2.5 cm, calculate BC, AB and AC.
The figure, given below, shows a trapezium ABCD. M and N are the mid-point of the non-parallel sides AD and BC respectively. Find:

- MN, if AB = 11 cm and DC = 8 cm.
- AB, if DC = 20 cm and MN = 27 cm.
- DC, if MN = 15 cm and AB = 23 cm.
In a triangle ABC, AD is a median and E is mid-point of median AD. A line through B and E meets AC at point F.
Prove that: AC = 3AF.
In Δ ABC, AD is the median and DE is parallel to BA, where E is a point in AC. Prove that BE is also a median.
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P.
Prove that:
(i) BP = 2AD
(ii) O is the mid-point of AP.
If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle,
show that the diagonals AC and BD intersect at the right angle.
E and F are respectively the mid-points of the non-parallel sides AD and BC of a trapezium ABCD. Prove that EF || AB and EF = `1/2` (AB + CD).
[Hint: Join BE and produce it to meet CD produced at G.]
