Advertisements
Advertisements
Question
The figure, given below, shows a trapezium ABCD. M and N are the mid-point of the non-parallel sides AD and BC respectively. Find:

- MN, if AB = 11 cm and DC = 8 cm.
- AB, if DC = 20 cm and MN = 27 cm.
- DC, if MN = 15 cm and AB = 23 cm.
Solution
Let we draw a diagonal AC as shown in the figure below,

(i) Given that AB = 11 cm, CD = 8 cm
From triangle ABC
ON = `[1]/[2]` AB
= `[1]/[2]` × 11
= 5.5 cm
From triangle ACD
OM = `[1]/[2]` CD
=`[1]/[2]` × 8
= 4 cm
Hence, MN = OM + ON
= (4 + 5.5)
= 9.5 cm
(ii) Given that CD = 20 cm, MN = 27 cm
From triangle ACD
OM = `[1]/[2]` CD
= `[1]/[2]` × 20
= 10 cm
Therefore, ON = 27 - 10 = 17 cm
From triangle ABC
AB = 2ON
= 2 × 17
= 34 cm
(iii) Given that AB = 23 cm, MN = 15 cm
From triangle ABC
ON =`[1]/[2]` AB
=`[1]/[2]` × 23
= 11.5 cm
OM = 15 - 11.5
OM = 3.5 cm
From triangle ACD
CD = 2OM
= 2 × 3.5
CD = 7 cm
APPEARS IN
RELATED QUESTIONS
In a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC =
21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ.
Let Abc Be an Isosceles Triangle in Which Ab = Ac. If D, E, F Be the Mid-points of the Sides Bc, Ca and a B Respectively, Show that the Segment Ad and Ef Bisect Each Other at Right Angles.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
L and M are the mid-point of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
A parallelogram ABCD has P the mid-point of Dc and Q a point of Ac such that
CQ = `[1]/[4]`AC. PQ produced meets BC at R.

Prove that
(i)R is the midpoint of BC
(ii) PR = `[1]/[2]` DB
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P.
Prove that:
(i) BP = 2AD
(ii) O is the mid-point of AP.
ABCD is a parallelogram.E is the mid-point of CD and P is a point on AC such that PC = `(1)/(4)"AC"`. EP produced meets BC at F. Prove that: F is the mid-point of BC.
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: The line drawn through G and parallel to FE and bisects DA.
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: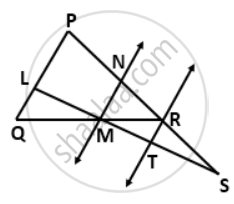
RT = `(1)/(3)"PQ"`
Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a square is also a square.
