Advertisements
Advertisements
Question
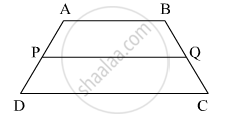
The following figure shows a trapezium ABCD in which AB // DC. P is the mid-point of AD and PR // AB. Prove that:
PR = `[1]/[2]` ( AB + CD)

Solution
Here from the triangle,
ABD P is the midpoint of AD and PR || AB,
therefore Q is the midpoint of BD
Similarly, R is the midpoint of BC as PR || CD || AB
From triangle ABD,
PQ = `1/2` AB ...(1) ...[by Mid-point theorem]
From triangle BCD,
QR = `1/2` CD ...(2) ...[by Mid-point theorem]
Now (1) + (2)
PQ + QR = `1/2 "AB" + 1/2 "CD"`
PR = `1/2`(AB + CD)
Hence proved.
APPEARS IN
RELATED QUESTIONS
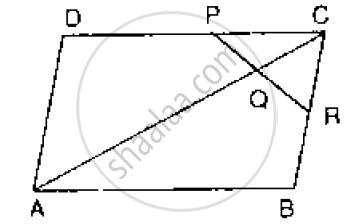
In below Fig, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.
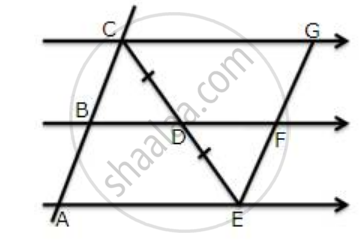
ABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP = PH
In the Figure, `square`ABCD is a trapezium. AB || DC. Points P and Q are midpoints of seg AD and seg BC respectively. Then prove that, PQ || AB and PQ = `1/2 ("AB" + "DC")`.
ABCD is a quadrilateral in which AD = BC. E, F, G and H are the mid-points of AB, BD, CD and Ac respectively. Prove that EFGH is a rhombus.

Use the following figure to find:
(i) BC, if AB = 7.2 cm.
(ii) GE, if FE = 4 cm.
(iii) AE, if BD = 4.1 cm
(iv) DF, if CG = 11 cm.
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find DE, if AB = 8 cm
Prove that the straight lines joining the mid-points of the opposite sides of a quadrilateral bisect each other.
In ΔABC, D and E are the midpoints of the sides AB and AC respectively. F is any point on the side BC. If DE intersects AF at P show that DP = PE.
P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD such that AC ⊥ BD. Prove that PQRS is a rectangle.
P, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC = BD and AC ⊥ BD. Prove that PQRS is a square.
