Advertisements
Advertisements
Question
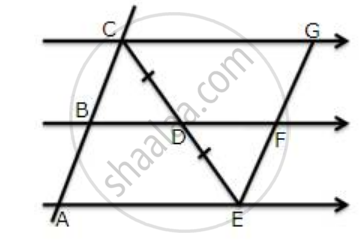
Use the following figure to find:
(i) BC, if AB = 7.2 cm.
(ii) GE, if FE = 4 cm.
(iii) AE, if BD = 4.1 cm
(iv) DF, if CG = 11 cm.
Solution
According to the equal intercept theorem since CD = DE
Therefore AB = BC and EF = GF
(i) BC = AB = 7.2cm
(ii) GE = EF + GF
= 2EF
= 2 x 4
=8cm
Since B, D, and F are the mid-point and AE || BF || CG
Therefore AE = 2BD and CG = 2DF
(iii) AE = 2BD
= 2 x 4.1
= 8.2
(iv) DF =
=
= 5.5 cm
APPEARS IN
RELATED QUESTIONS
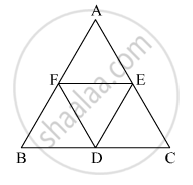
In the given figure, ΔABC is an equilateral traingle. Points F, D and E are midpoints of side AB, side BC, side AC respectively. Show that ΔFED is an equilateral traingle.
In the given figure, seg PD is a median of ΔPQR. Point T is the mid point of seg PD. Produced QT intersects PR at M. Show that
[Hint: DN || QM]

In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find FE, if BC = 14 cm
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find ∠FDB if ∠ACB = 115°.
D, E and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC. Prove that ΔDEF is also isosceles.
In parallelogram ABCD, P is the mid-point of DC. Q is a point on AC such that CQ =
(i) R is the mid-point of BC, and
(ii) PR =
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: The line drawn through G and parallel to FE and bisects DA.
In ΔABC, X is the mid-point of AB, and Y is the mid-point of AC. BY and CX are produced and meet the straight line through A parallel to BC at P and Q respectively. Prove AP = AQ.
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: A is the mid-point of PQ.
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: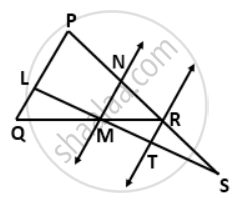
ST =
