Advertisements
Advertisements
प्रश्न
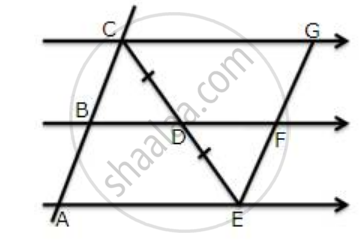
Use the following figure to find:
(i) BC, if AB = 7.2 cm.
(ii) GE, if FE = 4 cm.
(iii) AE, if BD = 4.1 cm
(iv) DF, if CG = 11 cm.
उत्तर
According to the equal intercept theorem since CD = DE
Therefore AB = BC and EF = GF
(i) BC = AB = 7.2cm
(ii) GE = EF + GF
= 2EF
= 2 x 4
=8cm
Since B, D, and F are the mid-point and AE || BF || CG
Therefore AE = 2BD and CG = 2DF
(iii) AE = 2BD
= 2 x 4.1
= 8.2
(iv) DF = `[1]/[2]`CG
= `[1]/[2]` x 11
= 5.5 cm
APPEARS IN
संबंधित प्रश्न
Fill in the blank to make the following statement correct
The triangle formed by joining the mid-points of the sides of an isosceles triangle is
In the Figure, `square`ABCD is a trapezium. AB || DC. Points P and Q are midpoints of seg AD and seg BC respectively. Then prove that, PQ || AB and PQ = `1/2 ("AB" + "DC")`.
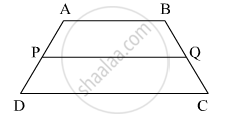
The figure, given below, shows a trapezium ABCD. M and N are the mid-point of the non-parallel sides AD and BC respectively. Find:

- MN, if AB = 11 cm and DC = 8 cm.
- AB, if DC = 20 cm and MN = 27 cm.
- DC, if MN = 15 cm and AB = 23 cm.
L and M are the mid-point of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square is also a square.
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: The line drawn through G and parallel to FE and bisects DA.
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
Show that AE and DF bisect each other.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: ΔHEB ≅ ΔHFC
The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only if, ______.
E is the mid-point of a median AD of ∆ABC and BE is produced to meet AC at F. Show that AF = `1/3` AC.
