Advertisements
Advertisements
प्रश्न
Fill in the blank to make the following statement correct
The triangle formed by joining the mid-points of the sides of an isosceles triangle is
उत्तर
Isosceles
APPEARS IN
संबंधित प्रश्न
ABCD is a rhombus, EABF is a straight line such that EA = AB = BF. Prove that ED and FC when produced meet at right angles
ABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively
intersecting at P, Q and R. Prove that the perimeter of ΔPQR is double the perimeter of
ΔABC
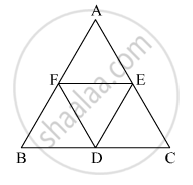
In the given figure, ΔABC is an equilateral traingle. Points F, D and E are midpoints of side AB, side BC, side AC respectively. Show that ΔFED is an equilateral traingle.
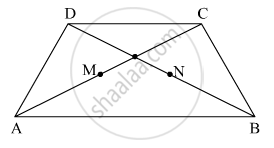
In the adjacent figure, `square`ABCD is a trapezium AB || DC. Points M and N are midpoints of diagonal AC and DB respectively then prove that MN || AB.
D and F are midpoints of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
- Prove that BDFE is a parallelogram
- Find AB, if EF = 4.8 cm.
In a triangle ABC, AD is a median and E is mid-point of median AD. A line through B and E meets AC at point F.
Prove that: AC = 3AF.
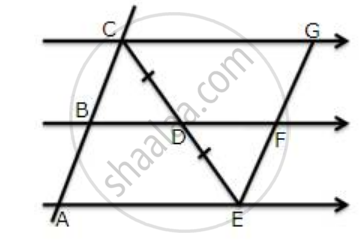
Use the following figure to find:
(i) BC, if AB = 7.2 cm.
(ii) GE, if FE = 4 cm.
(iii) AE, if BD = 4.1 cm
(iv) DF, if CG = 11 cm.
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square is also a square.
In ΔABC, P is the mid-point of BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that: AP = 2AR
P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.
