Advertisements
Advertisements
प्रश्न
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral
bisect each other.
उत्तर

Let ABCD is a quadrilateral in which P,Q, R and S are midpoints of sides
AB, BC,CD and DA respectively join PQ,QR,RS, SP and BD
In ABD, S and P are the midpoints of AD and AB respectively.
So, by using midpoint theorem we can say that
SP || BD and SP = `1/2` BD ......(1)
Similarly in ΔBCD
QR || BD and QR = `1/2` BD .....(2)
From equation (1) and (2) we have
SP || QR and SP = QR
As in quadrilateral SPQR one pair of opposite side are equal and parallel to each other. So, SPQR is parallelogram
Since, diagonals of a parallelogram bisect each other.
Hence PR and QS bisect each other.
APPEARS IN
संबंधित प्रश्न
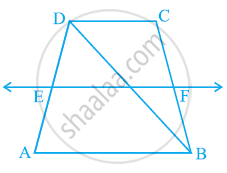
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
BM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If
L is the mid-point of BC, prove that LM = LN.
In the given figure, points X, Y, Z are the midpoints of side AB, side BC and side AC of ΔABC respectively. AB = 5 cm, AC = 9 cm and BC = 11 cm. Find the length of XY, YZ, XZ.

In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
L and M are the mid-point of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
In triangle ABC, P is the mid-point of side BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R.
Prove that : (i) AP = 2AR
(ii) BC = 4QR
In triangle ABC ; D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F.
Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm,
find the perimeter of the parallelogram BDEF.
D and E are the mid-points of the sides AB and AC of ∆ABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is ______.
D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral triangle ABC. Show that ∆DEF is also an equilateral triangle.
P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.
