Advertisements
Advertisements
प्रश्न
In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
उत्तर
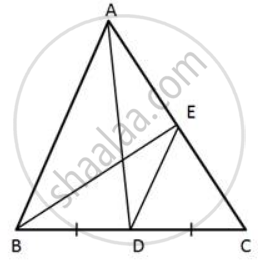
ln ΔABC,
AD is the median of BC.
⇒ D is the mid-point of BC.
Given at DE || BA
By the Converse of the Mid-point theorem,
⇒ DE bisects AC
⇒ E is the mid-point of AC
⇒ BE is the median of AC
that is BE is also a median.
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral
bisect each other.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
In ∆ABC, E is the mid-point of the median AD, and BE produced meets side AC at point Q.
Show that BE: EQ = 3: 1.
In Δ ABC, AD is the median and DE is parallel to BA, where E is a point in AC. Prove that BE is also a median.
In triangle ABC, the medians BP and CQ are produced up to points M and N respectively such that BP = PM and CQ = QN. Prove that:
- M, A, and N are collinear.
- A is the mid-point of MN.
If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle,
show that the diagonals AC and BD intersect at the right angle.
In ΔABC, BE and CF are medians. P is a point on BE produced such that BE = EP and Q is a point on CF produced such that CF = FQ. Prove that: QAP is a straight line.
D, E and F are respectively the mid-points of the sides AB, BC and CA of a triangle ABC. Prove that by joining these mid-points D, E and F, the triangles ABC is divided into four congruent triangles.
