Advertisements
Advertisements
प्रश्न
In ∆ABC, E is the mid-point of the median AD, and BE produced meets side AC at point Q.
Show that BE: EQ = 3: 1.
उत्तर
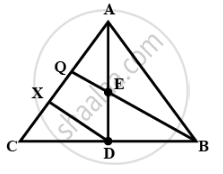
Construction: Draw DX || BQ
In ΔBCQ and ΔDCX,
∠BCQ = ∠DCX ...(Common)
∠BQC = ∠DXC ...(Corresponding angles)
So, ΔBCQ ∼ ΔDCX ....(AA Similarity criterion)
⇒ `"BQ"/"DX" = "BC"/"DC" = "CQ"/"CX"` ...(Corresponding sides are proportional.)
⇒ `"BQ"/"DX" = "2CD"/"CD"` ...(D is the mid-point of BC)
⇒ `"BQ"/"DX" = 2` ...(i)
Similarly, ΔAEQ ∼ ΔADX,
⇒ `"EQ"/"DX" = "AE"/"ED" = 1/2` ...(E is the mid-point of AD)
That is `"EQ"/"DX" = 1/2` ...(ii)
Dividing (i) by (ii), We get
⇒ `"BQ"/"EQ" = 4`
⇒ BE + EQ = 4EQ
⇒ BE = 3EQ
⇒ `"BQ"/"EQ" = 3/1`
APPEARS IN
संबंधित प्रश्न
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
In triangle ABC, M is mid-point of AB and a straight line through M and parallel to BC cuts AC in N. Find the lengths of AN and MN if Bc = 7 cm and Ac = 5 cm.
If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle,
show that the diagonals AC and BD intersect at the right angle.
In ΔABC, D is the mid-point of AB and E is the mid-point of BC.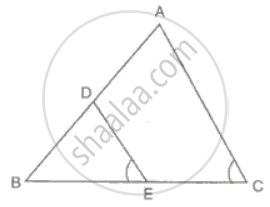
Calculate:
(i) DE, if AC = 8.6 cm
(ii) ∠DEB, if ∠ACB = 72°
In ΔABC, AB = 12 cm and AC = 9 cm. If M is the mid-point of AB and a straight line through M parallel to AC cuts BC in N, what is the length of MN?
Prove that the straight lines joining the mid-points of the opposite sides of a quadrilateral bisect each other.
In parallelogram ABCD, P is the mid-point of DC. Q is a point on AC such that CQ = `(1)/(4)"AC"`. PQ produced meets BC at R. Prove that
(i) R is the mid-point of BC, and
(ii) PR = `(1)/(2)"DB"`.
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: A is the mid-point of PQ.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rhombus, if ______.
E is the mid-point of the side AD of the trapezium ABCD with AB || DC. A line through E drawn parallel to AB intersect BC at F. Show that F is the mid-point of BC. [Hint: Join AC]
