Advertisements
Advertisements
प्रश्न
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: A is the mid-point of PQ.
उत्तर
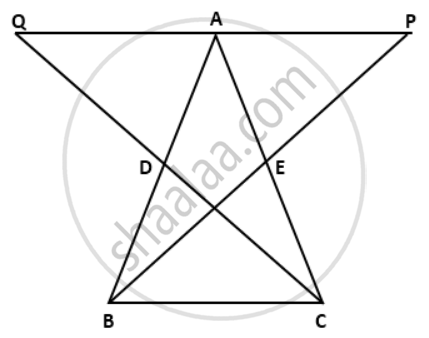
In ΔBDC and ΔADQ,
CD = DQ ....(given)
∠BDC = ∠ADQ ....(vertically opposite angles)
BD = AD ....(D is the mid-point of AB)
∴ ΔBDC ≅ ΔADQ
⇒ ∠DBC = ∠DAQ (c.p.c.t)....(i)
And, BC = AQ (c.p.c.t)....(ii)
Similarly, we can prove ΔCEB ≅ ΔAEP
⇒ ∠ECB = ∠EAP (c.p.c.t)....(iii)
And, BC = AP (c.p.c.t)....(iv)
From (ii) and (iv),
AQ = AP
⇒ A is the mid-point of PQ.
APPEARS IN
संबंधित प्रश्न
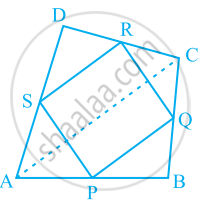
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see the given figure). AC is a diagonal. Show that:
- SR || AC and SR = `1/2AC`
- PQ = SR
- PQRS is a parallelogram.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
ABC is a triang D is a point on AB such that AD = `1/4` AB and E is a point on AC such that AE = `1/4` AC. Prove that DE = `1/4` BC.
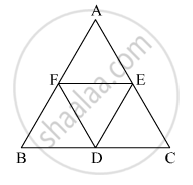
In the given figure, ΔABC is an equilateral traingle. Points F, D and E are midpoints of side AB, side BC, side AC respectively. Show that ΔFED is an equilateral traingle.
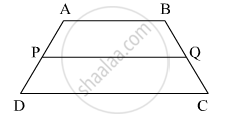
In the Figure, `square`ABCD is a trapezium. AB || DC. Points P and Q are midpoints of seg AD and seg BC respectively. Then prove that, PQ || AB and PQ = `1/2 ("AB" + "DC")`.
In triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
In ΔABC, D is the mid-point of AB and E is the mid-point of BC.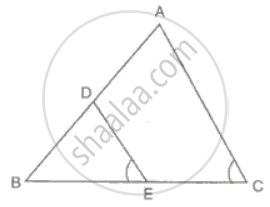
Calculate:
(i) DE, if AC = 8.6 cm
(ii) ∠DEB, if ∠ACB = 72°
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find DE, if AB = 8 cm
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: ΔHEB ≅ ΔHFC
E and F are respectively the mid-points of the non-parallel sides AD and BC of a trapezium ABCD. Prove that EF || AB and EF = `1/2` (AB + CD).
[Hint: Join BE and produce it to meet CD produced at G.]
