Advertisements
Advertisements
प्रश्न
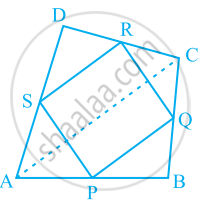
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see the given figure). AC is a diagonal. Show that:
- SR || AC and SR = `1/2AC`
- PQ = SR
- PQRS is a parallelogram.
उत्तर
(i) In ΔADC, S and R are the mid-points of sides AD and CD respectively.
In a triangle, the line segment joining the mid-points of any two sides of the triangle is parallel to the third side and is half of it.
∴ SR || AC and SR = `1/2AC` ...(1)
(ii) In ΔABC, P and Q are mid-points of sides AB and BC respectively. Therefore, by using the mid-point theorem,
PQ || AC and PQ = `1/2AC` ...(2)
Using equations (1) and (2), we obtain
PQ || SR and PQ = SR ...(3)
⇒ PQ = SR
(iii) From equation (3), we obtained
PQ || SR and PQ = SR
Clearly, one pair of opposite sides of quadrilateral PQRS is parallel and equal.
Hence, PQRS is a parallelogram.
APPEARS IN
संबंधित प्रश्न
In a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC =
21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ.
In Fig. below, BE ⊥ AC. AD is any line from A to BC intersecting BE in H. P, Q and R are
respectively the mid-points of AH, AB and BC. Prove that ∠PQR = 90°.

D, E, and F are the mid-points of the sides AB, BC, and CA respectively of ΔABC. AE meets DF at O. P and Q are the mid-points of OB and OC respectively. Prove that DPQF is a parallelogram.
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P.
Prove that:
(i) BP = 2AD
(ii) O is the mid-point of AP.
In the given figure, AD and CE are medians and DF // CE.
Prove that: FB = `1/4` AB.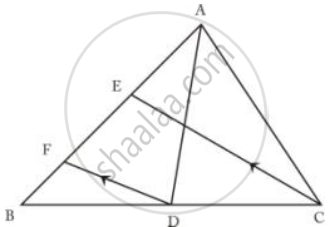
Prove that the straight lines joining the mid-points of the opposite sides of a quadrilateral bisect each other.
In a parallelogram ABCD, M is the mid-point AC. X and Y are the points on AB and DC respectively such that AX = CY. Prove that:
(i) Triangle AXM is congruent to triangle CYM, and
(ii) XMY is a straight line.
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
If AE and DF intersect at G, and M and N are the midpoints of GB and GC respectively, prove that DMNF is a parallelogram.
In ΔABC, D and E are the midpoints of the sides AB and AC respectively. F is any point on the side BC. If DE intersects AF at P show that DP = PE.
In the given figure, T is the midpoint of QR. Side PR of ΔPQR is extended to S such that R divides PS in the ratio 2:1. TV and WR are drawn parallel to PQ. Prove that T divides SU in the ratio 2:1 and WR = `(1)/(4)"PQ"`.
