Advertisements
Advertisements
प्रश्न
Prove that the straight lines joining the mid-points of the opposite sides of a quadrilateral bisect each other.
उत्तर
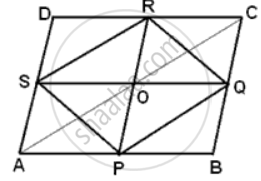
Join AC.
P and Q are mid-points of AB and BC respectively.
∴ PQ || AC, PQ = `(1)/(2)"AC"`.........(i)
S and R are mid-points of AD and DC respectively.
∴ SR || AC, SR = `(1)/(2)"AC"`.........(ii)
From (i) and (ii)
PQ = SR
Therefore, PQRS is a parallelogram.
Since, diagonals of a parallelogram bisect each other
Therefore, PQ and QS bisect each other.
APPEARS IN
संबंधित प्रश्न
In a triangle ∠ABC, ∠A = 50°, ∠B = 60° and ∠C = 70°. Find the measures of the angles of
the triangle formed by joining the mid-points of the sides of this triangle.
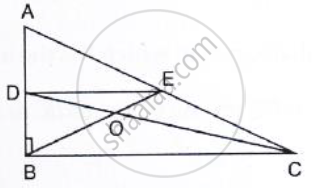
In Fig. below, triangle ABC is right-angled at B. Given that AB = 9 cm, AC = 15 cm and D,
E are the mid-points of the sides AB and AC respectively, calculate
(i) The length of BC (ii) The area of ΔADE.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral
bisect each other.
Fill in the blank to make the following statement correct
The triangle formed by joining the mid-points of the sides of an isosceles triangle is
In the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF.
Show that: EF = AC.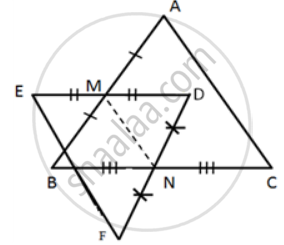
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P.
Prove that:
(i) BP = 2AD
(ii) O is the mid-point of AP.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: PQ, if AB = 12 cm and DC = 10 cm.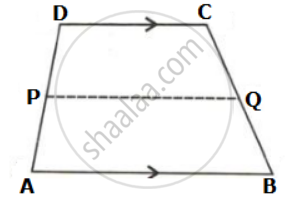
Side AC of a ABC is produced to point E so that CE = `(1)/(2)"AC"`. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meets AC at point P and EF at point R respectively. Prove that: 3DF = EF
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
If AE and DF intersect at G, and M and N are the midpoints of GB and GC respectively, prove that DMNF is a parallelogram.
P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.
