Advertisements
Advertisements
प्रश्न
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: PQ, if AB = 12 cm and DC = 10 cm.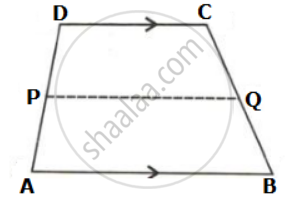
उत्तर
Let us draw a diagonal AC which meets PQ at O as shown below: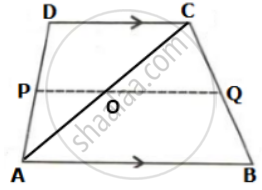
Given AB = 12 cm and DC = 10 cm
In ΔABC,
OQ = `(1)/(2)"AB"` ....(Mid-point Theorem)
⇒ OQ = `(1)/(2) xx 12` = 6 cm
In ΔADC,
OP = `(1)/(2)"DC"` ....(Mid-point Theorem)
⇒ OP = `(1)/(2) xx 10` = 5 cm
Now,
PQ = OP + OQ
= 6 + 5
= 11 cm.
APPEARS IN
संबंधित प्रश्न
In a triangle ∠ABC, ∠A = 50°, ∠B = 60° and ∠C = 70°. Find the measures of the angles of
the triangle formed by joining the mid-points of the sides of this triangle.
ABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP = PH
In the given figure, points X, Y, Z are the midpoints of side AB, side BC and side AC of ΔABC respectively. AB = 5 cm, AC = 9 cm and BC = 11 cm. Find the length of XY, YZ, XZ.

In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle,
show that the diagonals AC and BD intersect at the right angle.
ABCD is a parallelogram.E is the mid-point of CD and P is a point on AC such that PC = `(1)/(4)"AC"`. EP produced meets BC at F. Prove that: F is the mid-point of BC.
In AABC, D and E are two points on the side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet the side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meet the side BC at points M and N respectively. Prove that BM = MN = NC.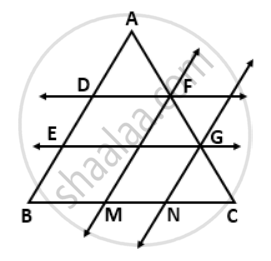
In ΔABC, D and E are the midpoints of the sides AB and AC respectively. F is any point on the side BC. If DE intersects AF at P show that DP = PE.
E is the mid-point of a median AD of ∆ABC and BE is produced to meet AC at F. Show that AF = `1/3` AC.
D, E and F are respectively the mid-points of the sides AB, BC and CA of a triangle ABC. Prove that by joining these mid-points D, E and F, the triangles ABC is divided into four congruent triangles.
