Advertisements
Chapters
2: Profit , Loss and Discount
3: Compound Interest
4: Expansions
5: Factorisation
6: Changing the subject of a formula
7: Linear Equations
8: Simultaneous Linear Equations
9: Indices
10: Logarithms
11: Triangles and their congruency
12: Isosceles Triangle
13: Inequalities in Triangles
14: Constructions of Triangles
▶ 15: Mid-point and Intercept Theorems
16: Similarity
17: Pythagoras Theorem
18: Rectilinear Figures
19: Quadrilaterals
20: Constructions of Quadrilaterals
21: Areas Theorems on Parallelograms
22: Statistics
23: Graphical Representation of Statistical Data
24: Perimeter and Area
25: Surface Areas and Volume of Solids
26: Trigonometrical Ratios
27: Trigonometrical Ratios of Standard Angles
28: Coordinate Geometry
![Frank solutions for Mathematics [English] Class 9 ICSE chapter 15 - Mid-point and Intercept Theorems Frank solutions for Mathematics [English] Class 9 ICSE chapter 15 - Mid-point and Intercept Theorems - Shaalaa.com](/images/mathematics-english-class-9-icse_6:c41cc344f5174c64a036c55d113af73f.jpg)
Advertisements
Solutions for Chapter 15: Mid-point and Intercept Theorems
Below listed, you can find solutions for Chapter 15 of CISCE Frank for Mathematics [English] Class 9 ICSE.
Frank solutions for Mathematics [English] Class 9 ICSE 15 Mid-point and Intercept Theorems Exercise 15.1
In ΔABC, D is the mid-point of AB and E is the mid-point of BC.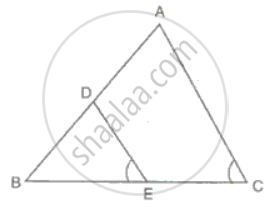
Calculate:
(i) DE, if AC = 8.6 cm
(ii) ∠DEB, if ∠ACB = 72°
In ΔABC, AB = 12 cm and AC = 9 cm. If M is the mid-point of AB and a straight line through M parallel to AC cuts BC in N, what is the length of MN?
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find FE, if BC = 14 cm
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find DE, if AB = 8 cm
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find ∠FDB if ∠ACB = 115°.
In parallelogram PQRS, L is mid-point of side SR and SN is drawn parallel to LQ which meets RQ produced at N and cuts side PQ at M. Prove that M is the mid-point of PQ.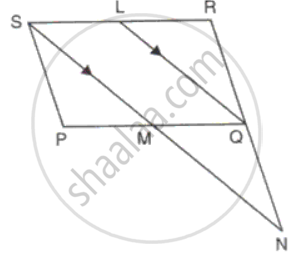
In ΔABC, BE and CF are medians. P is a point on BE produced such that BE = EP and Q is a point on CF produced such that CF = FQ. Prove that: QAP is a straight line.
In ΔABC, BE and CF are medians. P is a point on BE produced such that BE = EP and Q is a point on CF produced such that CF = FQ. Prove that: A is the mid-point of PQ.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
D, E and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC. Prove that ΔDEF is also isosceles.
Prove that the straight lines joining the mid-points of the opposite sides of a quadrilateral bisect each other.
The diagonals of a quadrilateral intersect each other at right angle. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.
If L and M are the mid-points of AB, and DC respectively of parallelogram ABCD. Prove that segment DL and BM trisect diagonal AC.
In a right-angled triangle ABC. ∠ABC = 90° and D is the midpoint of AC. Prove that BD = `(1)/(2)"AC"`.
In parallelogram ABCD, P is the mid-point of DC. Q is a point on AC such that CQ = `(1)/(4)"AC"`. PQ produced meets BC at R. Prove that
(i) R is the mid-point of BC, and
(ii) PR = `(1)/(2)"DB"`.
In a parallelogram ABCD, M is the mid-point AC. X and Y are the points on AB and DC respectively such that AX = CY. Prove that:
(i) Triangle AXM is congruent to triangle CYM, and
(ii) XMY is a straight line.
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square is also a square.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: PQ, if AB = 12 cm and DC = 10 cm.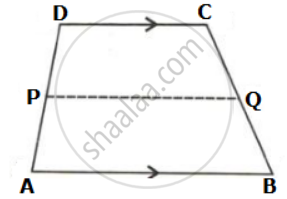
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: AB, if DC = 8 cm and PQ = 9.5 cm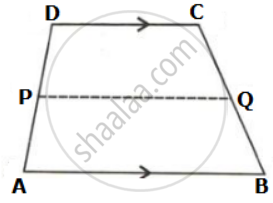
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: DC, if AB = 20 cm and PQ = 14 cm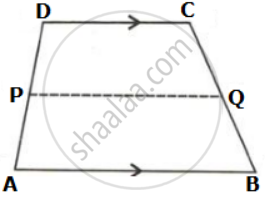
In ΔABC, P is the mid-point of BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that: AP = 2AR
In ΔABC, P is the mid-point of BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that: BC = 4QR
Side AC of a ABC is produced to point E so that CE = `(1)/(2)"AC"`. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meets AC at point P and EF at point R respectively. Prove that: 3DF = EF
Side AC of a ABC is produced to point E so that CE = `(1)/(2)"AC"`. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meets AC at point P and EF at point R respectively. Prove that: 4CR = AB.
AD is a median of side BC of ABC. E is the midpoint of AD. BE is joined and produced to meet AC at F. Prove that AF: AC = 1 : 3.
M and N divide the side AB of ΔABC into three equal parts. Line segments MP and NQ are both parallel to BC, and meet AC in P and Q respectively. Prove that P and Q divide AC into three equal parts.
ΔABC is an isosceles triangle with AB = AC. D, E and F are the mid-points of BC, AB and AC respectively. Prove that the line segment AD is perpendicular to EF and is bisected by it.
ABCD is a parallelogram.E is the mid-point of CD and P is a point on AC such that PC = `(1)/(4)"AC"`. EP produced meets BC at F. Prove that: F is the mid-point of BC.
ABCD is a parallelogram.E is the mid-point of CD and P is a point on AC such that PC = `(1)/(4)"AC"`. EP produced meets BC at F. Prove that: 2EF = BD.
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: ∠EFG = 90°
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: The line drawn through G and parallel to FE and bisects DA.
In ΔABC, X is the mid-point of AB, and Y is the mid-point of AC. BY and CX are produced and meet the straight line through A parallel to BC at P and Q respectively. Prove AP = AQ.
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
Show that AE and DF bisect each other.
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
If AE and DF intersect at G, and M and N are the midpoints of GB and GC respectively, prove that DMNF is a parallelogram.
Frank solutions for Mathematics [English] Class 9 ICSE 15 Mid-point and Intercept Theorems Exercise 15.2
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: ΔGEA ≅ ΔGFD
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: ΔHEB ≅ ΔHFC
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: EGFH is a parallelogram.
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: Q A and P are collinear.
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: A is the mid-point of PQ.
In AABC, D and E are two points on the side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet the side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meet the side BC at points M and N respectively. Prove that BM = MN = NC.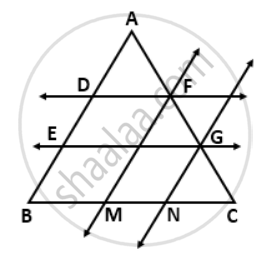
In the given figure, the lines l, m and n are parallel to each other. D is the midpoint of CE. Find: a. BC, b. EF, c. CG and d. BD.
The diagonals AC and BD of a quadrilateral ABCD intersect at right angles. Prove that the quadrilateral formed by joining the midpoints of quadrilateral ABCD is a rectangle.
In ΔABC, D and E are the midpoints of the sides AB and AC respectively. F is any point on the side BC. If DE intersects AF at P show that DP = PE.
In ΔABC, D and E are the midpoints of the sides AB and BC respectively. F is any point on the side AC. Also, EF is parallel to AB. Prove that BFED is a parallelogram.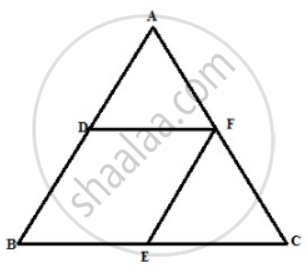
Remark: Figure is incorrect in Question
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: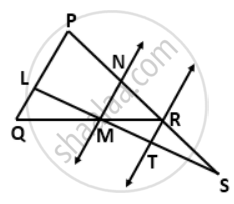
ST = `(1)/(3)"LS"`
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: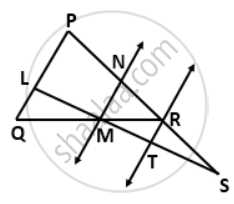
RT = `(1)/(3)"PQ"`
In the given figure, T is the midpoint of QR. Side PR of ΔPQR is extended to S such that R divides PS in the ratio 2:1. TV and WR are drawn parallel to PQ. Prove that T divides SU in the ratio 2:1 and WR = `(1)/(4)"PQ"`.
Solutions for 15: Mid-point and Intercept Theorems
![Frank solutions for Mathematics [English] Class 9 ICSE chapter 15 - Mid-point and Intercept Theorems Frank solutions for Mathematics [English] Class 9 ICSE chapter 15 - Mid-point and Intercept Theorems - Shaalaa.com](/images/mathematics-english-class-9-icse_6:c41cc344f5174c64a036c55d113af73f.jpg)
Frank solutions for Mathematics [English] Class 9 ICSE chapter 15 - Mid-point and Intercept Theorems
Shaalaa.com has the CISCE Mathematics Mathematics [English] Class 9 ICSE CISCE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Frank solutions for Mathematics Mathematics [English] Class 9 ICSE CISCE 15 (Mid-point and Intercept Theorems) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Frank textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 9 ICSE chapter 15 Mid-point and Intercept Theorems are Theorem of Midpoints of Two Sides of a Triangle, Equal Intercept Theorem.
Using Frank Mathematics [English] Class 9 ICSE solutions Mid-point and Intercept Theorems exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Frank Solutions are essential questions that can be asked in the final exam. Maximum CISCE Mathematics [English] Class 9 ICSE students prefer Frank Textbook Solutions to score more in exams.
Get the free view of Chapter 15, Mid-point and Intercept Theorems Mathematics [English] Class 9 ICSE additional questions for Mathematics Mathematics [English] Class 9 ICSE CISCE, and you can use Shaalaa.com to keep it handy for your exam preparation.
