Advertisements
Advertisements
प्रश्न
In a right-angled triangle ABC. ∠ABC = 90° and D is the midpoint of AC. Prove that BD = `(1)/(2)"AC"`.
उत्तर
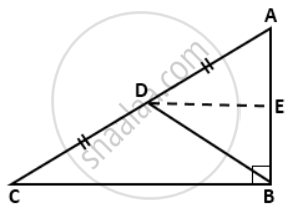
Draw line segment DE || CB, which meets AB at point E.
Now, DE || CB and AB is the transversal,
∴ ∠AED = ∠ABC ....(corrresponding angles)
∠ABC = 90° ....(given)
⇒ ∠AED = 90°
Also, as D is the mid-point of AC and DE || CB,
DE bisects side AB,
I.e. AE = BE ....(i)
In ΔAED and ΔBED,
∠AED = ∠BED ....(Each 90°)
AE = BE ....[From (i)]
DE = DE ....(Common)
∴ ΔAED ≅ ΔBEd ....(By SAS Test)
⇒ AD = BD ....(C.P.C.T.C)
⇒ BD = AC
⇒ BD = `(1)/(2)"AC"`.
APPEARS IN
संबंधित प्रश्न
In a ΔABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC
intersects FE at Q. Prove that AQ = QP.
In a ΔABC, BM and CN are perpendiculars from B and C respectively on any line passing
through A. If L is the mid-point of BC, prove that ML = NL.
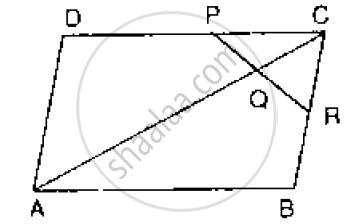
In below Fig, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.
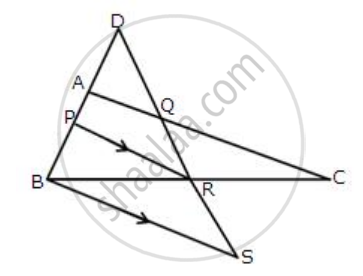
In the figure, give below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that:
(i) AQ // BS
(ii) DS = 3 Rs.
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P.
Prove that:
(i) BP = 2AD
(ii) O is the mid-point of AP.
In triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meets side BC at points M and N respectively. Prove that: BM = MN = NC.
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find ∠FDB if ∠ACB = 115°.
The diagonals of a quadrilateral intersect each other at right angle. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: PQ, if AB = 12 cm and DC = 10 cm.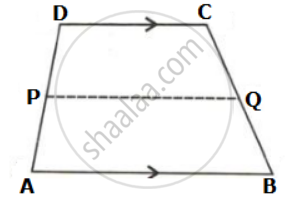
In the given figure, T is the midpoint of QR. Side PR of ΔPQR is extended to S such that R divides PS in the ratio 2:1. TV and WR are drawn parallel to PQ. Prove that T divides SU in the ratio 2:1 and WR = `(1)/(4)"PQ"`.
