Advertisements
Advertisements
प्रश्न
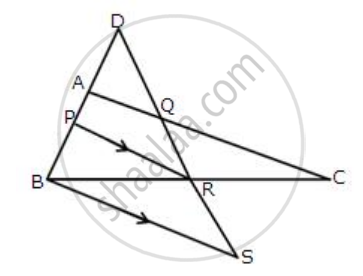
In the figure, give below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that:
(i) AQ // BS
(ii) DS = 3 Rs.
उत्तर
Given that AD = AP = PB as 2AD = AB and p is the midpoint of AB
(i) From triangle DPR, A and Q are the mid-point of DP and DR.
Therefore AQ || PR
Since PR || BS ,hence AQ || BS
(ii) From triangle ABC, P is the midpoint and PR || BS
Therefore R is the mid-point of BC
From ΔBRS and ΔQRC
∠BRS = ∠QRC
BR = RC
∠RBS + ∠RCQ
∴ ΔBRS ≅ ΔQRC
∴ QR =RS
DS = DQ + QR + RS = QR + QR + RS = 3RS
APPEARS IN
संबंधित प्रश्न
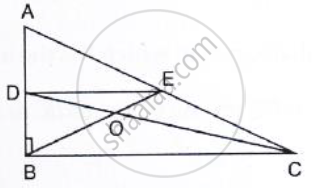
In Fig. below, triangle ABC is right-angled at B. Given that AB = 9 cm, AC = 15 cm and D,
E are the mid-points of the sides AB and AC respectively, calculate
(i) The length of BC (ii) The area of ΔADE.
ABCD is a kite having AB = AD and BC = CD. Prove that the figure formed by joining the
mid-points of the sides, in order, is a rectangle.
Let Abc Be an Isosceles Triangle in Which Ab = Ac. If D, E, F Be the Mid-points of the Sides Bc, Ca and a B Respectively, Show that the Segment Ad and Ef Bisect Each Other at Right Angles.
In the given figure, seg PD is a median of ΔPQR. Point T is the mid point of seg PD. Produced QT intersects PR at M. Show that `"PM"/"PR" = 1/3`.
[Hint: DN || QM]

In triangle ABC, the medians BP and CQ are produced up to points M and N respectively such that BP = PM and CQ = QN. Prove that:
- M, A, and N are collinear.
- A is the mid-point of MN.
In triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meets side BC at points M and N respectively. Prove that: BM = MN = NC.
In triangle ABC ; D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F.
Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm,
find the perimeter of the parallelogram BDEF.
In ΔABC, AB = 12 cm and AC = 9 cm. If M is the mid-point of AB and a straight line through M parallel to AC cuts BC in N, what is the length of MN?
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: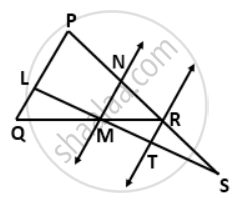
ST = `(1)/(3)"LS"`
P, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC = BD and AC ⊥ BD. Prove that PQRS is a square.
