Advertisements
Advertisements
प्रश्न
ABCD is a kite having AB = AD and BC = CD. Prove that the figure formed by joining the
mid-points of the sides, in order, is a rectangle.
उत्तर

Given,
A kite ABCD having AB = AD and BC = CD. P,Q,R, S are the midpoint of sides
AB,BC,CD andDArespectively PQ,QR,RS and spare joined
To prove:
PQRS is a rectangle
Proof:
In ΔABC, P and Q are the midpoints of AB and BC respectively.
∴PQ || AC and PQ = `1/2` AC ....(i )
In Δ ADC, R and S are the midpoint of CD and AD respectively.
∴ RS || AC and RS = `1/2` AC .....(ii )
From (i) and (ii), we have
PQ || RS and PQ = RS
Thus, in quadrilateral PQRS, a pair of opposite sides are equal and parallel. So PQRS is a
parallelogram. Now, we shall prove that one angle of parallelogram PQRS it is a right angle
Since AB = AD
⇒ `1/2` AB = AD `(1/2)`
⇒ AP = AS ...(iii) [∵ P and S are the midpoints of B and AD respectively]
⇒ `∠`1 = `∠`2 ....(iv)
Now, in ΔPBQ and ΔSDR, we have
PB = SD [ ∴AD = AB ⇒ `1/2` AD = `1/2` AB ]
BQ = DR ∴ PB = SD
And PQ = SR [ ∴ PQRS is a parallelogram]
So by SSS criterion of congruence, we have
Δ PBQ ≅ Δ SOR
⇒ `∠`3 = `∠`4 [CPCT ]
Now, `∠`3 + `∠`SPQ + `∠`2 = 180°
And `∠`1+ `∠`PSR + `∠`4 =180°
∴ `∠`3 + `∠`SPQ + `∠`2 = `∠`1+ `∠`PSR + `∠`4
⇒ `∠`SPQ = `∠`PSR (`∠`1 = `∠`2 and `∠`3 = `∠`4)
Now, transversal PS cuts parallel lines SR and PQ at S and P respectively.
∴ `∠`SPQ + `∠`PSR = 180°
⇒ 2`∠`SPQ = 180° = `∠`SPQ = 90° [ ∵ `∠`PSR = `∠`SPQ]
Thus, PQRS is a parallelogram such that `∠`SPQ = 90°
Hence, PQRS is a parallelogram.
APPEARS IN
संबंधित प्रश्न
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see the given figure). AC is a diagonal. Show that:
- SR || AC and SR = `1/2AC`
- PQ = SR
- PQRS is a parallelogram.
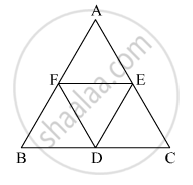
In the given figure, ΔABC is an equilateral traingle. Points F, D and E are midpoints of side AB, side BC, side AC respectively. Show that ΔFED is an equilateral traingle.
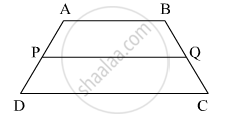
In the Figure, `square`ABCD is a trapezium. AB || DC. Points P and Q are midpoints of seg AD and seg BC respectively. Then prove that, PQ || AB and PQ = `1/2 ("AB" + "DC")`.
In the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF.
Show that: EF = AC.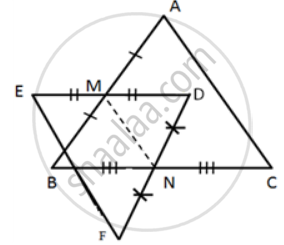
L and M are the mid-point of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
In triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meets side BC at points M and N respectively. Prove that: BM = MN = NC.
If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle,
show that the diagonals AC and BD intersect at the right angle.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
In the given figure, T is the midpoint of QR. Side PR of ΔPQR is extended to S such that R divides PS in the ratio 2:1. TV and WR are drawn parallel to PQ. Prove that T divides SU in the ratio 2:1 and WR = `(1)/(4)"PQ"`.
Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a square is also a square.
