Advertisements
Advertisements
प्रश्न
ABCD is a kite having AB = AD and BC = CD. Prove that the figure formed by joining the
mid-points of the sides, in order, is a rectangle.
उत्तर

Given,
A kite ABCD having AB = AD and BC = CD. P,Q,R, S are the midpoint of sides
AB,BC,CD andDArespectively PQ,QR,RS and spare joined
To prove:
PQRS is a rectangle
Proof:
In ΔABC, P and Q are the midpoints of AB and BC respectively.
∴PQ || AC and PQ = `1/2` AC ....(i )
In Δ ADC, R and S are the midpoint of CD and AD respectively.
∴ RS || AC and RS = `1/2` AC .....(ii )
From (i) and (ii), we have
PQ || RS and PQ = RS
Thus, in quadrilateral PQRS, a pair of opposite sides are equal and parallel. So PQRS is a
parallelogram. Now, we shall prove that one angle of parallelogram PQRS it is a right angle
Since AB = AD
⇒ `1/2` AB = AD `(1/2)`
⇒ AP = AS ...(iii) [∵ P and S are the midpoints of B and AD respectively]
⇒ `∠`1 = `∠`2 ....(iv)
Now, in ΔPBQ and ΔSDR, we have
PB = SD [ ∴AD = AB ⇒ `1/2` AD = `1/2` AB ]
BQ = DR ∴ PB = SD
And PQ = SR [ ∴ PQRS is a parallelogram]
So by SSS criterion of congruence, we have
Δ PBQ ≅ Δ SOR
⇒ `∠`3 = `∠`4 [CPCT ]
Now, `∠`3 + `∠`SPQ + `∠`2 = 180°
And `∠`1+ `∠`PSR + `∠`4 =180°
∴ `∠`3 + `∠`SPQ + `∠`2 = `∠`1+ `∠`PSR + `∠`4
⇒ `∠`SPQ = `∠`PSR (`∠`1 = `∠`2 and `∠`3 = `∠`4)
Now, transversal PS cuts parallel lines SR and PQ at S and P respectively.
∴ `∠`SPQ + `∠`PSR = 180°
⇒ 2`∠`SPQ = 180° = `∠`SPQ = 90° [ ∵ `∠`PSR = `∠`SPQ]
Thus, PQRS is a parallelogram such that `∠`SPQ = 90°
Hence, PQRS is a parallelogram.
APPEARS IN
संबंधित प्रश्न
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
ABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE = BF = CG = DH. Prove that EFGH is a square.
In below Fig, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.
Fill in the blank to make the following statement correct:
The triangle formed by joining the mid-points of the sides of a right triangle is
In trapezium ABCD, AB is parallel to DC; P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E.
Prove that:
- Point P bisects BE,
- PQ is parallel to AB.
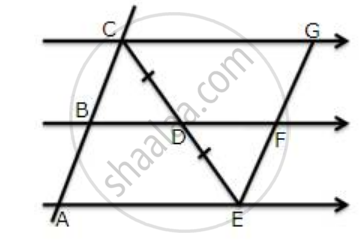
Use the following figure to find:
(i) BC, if AB = 7.2 cm.
(ii) GE, if FE = 4 cm.
(iii) AE, if BD = 4.1 cm
(iv) DF, if CG = 11 cm.
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P.
Prove that:
(i) BP = 2AD
(ii) O is the mid-point of AP.
In ΔABC, D is the mid-point of AB and E is the mid-point of BC.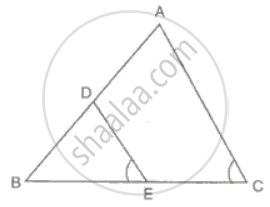
Calculate:
(i) DE, if AC = 8.6 cm
(ii) ∠DEB, if ∠ACB = 72°
AD is a median of side BC of ABC. E is the midpoint of AD. BE is joined and produced to meet AC at F. Prove that AF: AC = 1 : 3.
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: A is the mid-point of PQ.
