Advertisements
Advertisements
प्रश्न
In the Figure, `square`ABCD is a trapezium. AB || DC. Points P and Q are midpoints of seg AD and seg BC respectively. Then prove that, PQ || AB and PQ = `1/2 ("AB" + "DC")`.
उत्तर
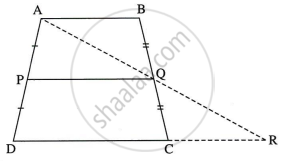
Given: `square`ABCD is a trapezium.
To prove: PQ || AB and PQ = `1/2`(AB + DC)
Construction: Extend line AQ in such a way that, on extending side DC, intersect it at point R.
Proof:
seg AB || seg DC ...(Given)
and seg BC is their transversal.
∴ ∠ABC ≅ ∠RCB ...(Alternate angles)
∴ ∠ABQ ≅ ∠RCQ ...(i) ...(B-Q-C)
In ∆ABQ and ∆RCQ,
∠ABQ ≅∠RCQ ...[From (i)]
seg BQ ≅ seg CQ ...(Q is the midpoint of seg BC)
∠BQA ≅ ∠CQR ...(Vertically opposite angles)
∴ ∆ABQ ≅ ∆RCQ ...(ASA test)
seg AB ≅ seg CR ...(c.s.c.t.) ...(ii)
seg AQ ≅ seg RQ ...(c.s.c.t.) ...(iii)
In ∆ADR,
Point P is the midpoint of line AD. ...(Given)
Point Q is the midpoint of line AR. ...[From (iii)]
∴ seg PQ || side DR ...(Midpoint Theorem)
∴ seg PQ || side DC ...(iv) ...(D-C-R)
∴ side AB || side DC ...(v) ...(Given)
∴ seg PQ || side AB ...[From (iv) and (v)]
PQ = `1/2` DR ...(Midpoint Theorem)
= `1/2` (DC + CR)
= `1/2` (DC + AB) ...[From (ii)]
∴ PQ = `1/2` (AB + DC)
APPEARS IN
संबंधित प्रश्न
In a triangle ∠ABC, ∠A = 50°, ∠B = 60° and ∠C = 70°. Find the measures of the angles of
the triangle formed by joining the mid-points of the sides of this triangle.
BM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If
L is the mid-point of BC, prove that LM = LN.
D and F are midpoints of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
- Prove that BDFE is a parallelogram
- Find AB, if EF = 4.8 cm.
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P.
Prove that:
(i) BP = 2AD
(ii) O is the mid-point of AP.
In parallelogram PQRS, L is mid-point of side SR and SN is drawn parallel to LQ which meets RQ produced at N and cuts side PQ at M. Prove that M is the mid-point of PQ.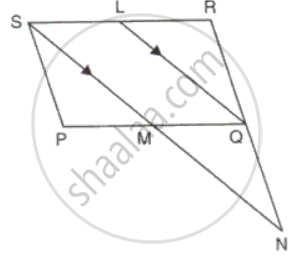
In ΔABC, BE and CF are medians. P is a point on BE produced such that BE = EP and Q is a point on CF produced such that CF = FQ. Prove that: QAP is a straight line.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
If L and M are the mid-points of AB, and DC respectively of parallelogram ABCD. Prove that segment DL and BM trisect diagonal AC.
In ∆ABC, AB = 5 cm, BC = 8 cm and CA = 7 cm. If D and E are respectively the mid-points of AB and BC, determine the length of DE.
Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a square is also a square.
