Advertisements
Advertisements
प्रश्न
In parallelogram PQRS, L is mid-point of side SR and SN is drawn parallel to LQ which meets RQ produced at N and cuts side PQ at M. Prove that M is the mid-point of PQ.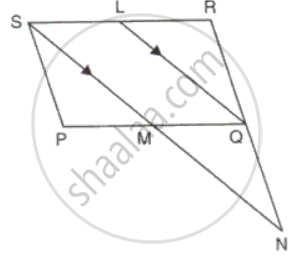
उत्तर
In ΔNSR
MQ = `(1)/(2)"SR"`
But L is the mid-point of SR and SR = PQ ...(sides of a parallelogram)
MQ = `(1)/(2)"PQ"`
MQ = PM = LS = LR
Therefore, M is the mid-point of PQ.
APPEARS IN
संबंधित प्रश्न
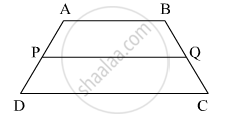
In the Figure, `square`ABCD is a trapezium. AB || DC. Points P and Q are midpoints of seg AD and seg BC respectively. Then prove that, PQ || AB and PQ = `1/2 ("AB" + "DC")`.
L and M are the mid-point of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
In triangle ABC, the medians BP and CQ are produced up to points M and N respectively such that BP = PM and CQ = QN. Prove that:
- M, A, and N are collinear.
- A is the mid-point of MN.
In trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that: AB + DC = 2EF.
In ΔABC, D is the mid-point of AB and E is the mid-point of BC.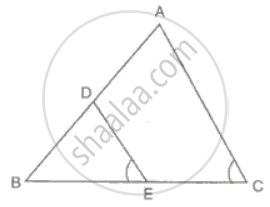
Calculate:
(i) DE, if AC = 8.6 cm
(ii) ∠DEB, if ∠ACB = 72°
In ΔABC, BE and CF are medians. P is a point on BE produced such that BE = EP and Q is a point on CF produced such that CF = FQ. Prove that: A is the mid-point of PQ.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
ABCD is a parallelogram.E is the mid-point of CD and P is a point on AC such that PC = `(1)/(4)"AC"`. EP produced meets BC at F. Prove that: F is the mid-point of BC.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: ΔGEA ≅ ΔGFD
D, E and F are respectively the mid-points of the sides AB, BC and CA of a triangle ABC. Prove that by joining these mid-points D, E and F, the triangles ABC is divided into four congruent triangles.
