Advertisements
Advertisements
प्रश्न
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: ΔGEA ≅ ΔGFD
उत्तर
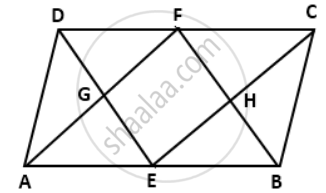
Since ABCD is a parallelogram,
AB = CD and AD = BC
Now, E and F are the mid-points of AB and CD respectively,
⇒ AE = EB = DF = FC ....(i)
In ΔGEA and ΔGFD,
AE = DF ....[From (i)]
∠AGE = ∠DGF ....(vertically opposite angles)
∠GAE = ∠GFD ....(Alternate interior angles)
∴ ΔGEA ≅ ΔGFD.
APPEARS IN
संबंधित प्रश्न
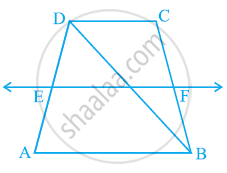
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
Fill in the blank to make the following statement correct:
The triangle formed by joining the mid-points of the sides of a right triangle is
The side AC of a triangle ABC is produced to point E so that CE = AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively.
Prove that:
- 3DF = EF
- 4CR = AB
ABCD is a parallelogram.E is the mid-point of CD and P is a point on AC such that PC = `(1)/(4)"AC"`. EP produced meets BC at F. Prove that: 2EF = BD.
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: ∠EFG = 90°
In ΔABC, D and E are the midpoints of the sides AB and BC respectively. F is any point on the side AC. Also, EF is parallel to AB. Prove that BFED is a parallelogram.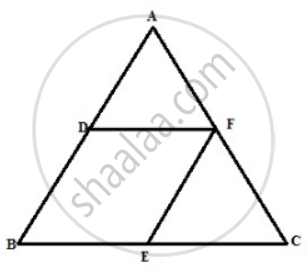
Remark: Figure is incorrect in Question
D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral triangle ABC. Show that ∆DEF is also an equilateral triangle.
P, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC = BD and AC ⊥ BD. Prove that PQRS is a square.
P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.
D, E and F are respectively the mid-points of the sides AB, BC and CA of a triangle ABC. Prove that by joining these mid-points D, E and F, the triangles ABC is divided into four congruent triangles.
