Advertisements
Advertisements
Question
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: ΔGEA ≅ ΔGFD
Solution
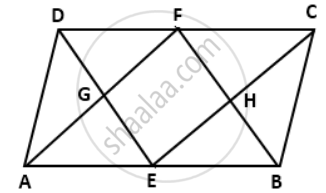
Since ABCD is a parallelogram,
AB = CD and AD = BC
Now, E and F are the mid-points of AB and CD respectively,
⇒ AE = EB = DF = FC ....(i)
In ΔGEA and ΔGFD,
AE = DF ....[From (i)]
∠AGE = ∠DGF ....(vertically opposite angles)
∠GAE = ∠GFD ....(Alternate interior angles)
∴ ΔGEA ≅ ΔGFD.
APPEARS IN
RELATED QUESTIONS
In a triangle ∠ABC, ∠A = 50°, ∠B = 60° and ∠C = 70°. Find the measures of the angles of
the triangle formed by joining the mid-points of the sides of this triangle.
In triangle ABC, the medians BP and CQ are produced up to points M and N respectively such that BP = PM and CQ = QN. Prove that:
- M, A, and N are collinear.
- A is the mid-point of MN.
In triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find ∠FDB if ∠ACB = 115°.
The diagonals of a quadrilateral intersect each other at right angle. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square is also a square.
In ΔABC, P is the mid-point of BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that: BC = 4QR
The diagonals AC and BD of a quadrilateral ABCD intersect at right angles. Prove that the quadrilateral formed by joining the midpoints of quadrilateral ABCD is a rectangle.
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: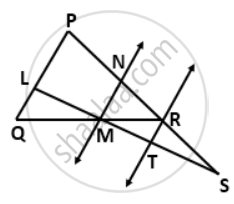
RT = `(1)/(3)"PQ"`
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rhombus, if ______.
