Advertisements
Advertisements
Question
In a triangle ∠ABC, ∠A = 50°, ∠B = 60° and ∠C = 70°. Find the measures of the angles of
the triangle formed by joining the mid-points of the sides of this triangle.
Solution

In ΔABC
D and E are midpoints of AB and BC
By midpoint theorem
∴ DE || AC, DE = `1/2` AC.
F is the midpoint of AC
Then, DE = `1/2` AC = CF
In a quadrilateral DECF
DE || AC, DE = CF
Hence DECF is a parallelogram
∴`∠`C = `∠`D = 70° [Opposite sides of parallelogram]
Similarly
BEFD is a parallelogram, `∠`B = `∠`F = 60°
ADEF is a parallelogram, `∠`A = `∠`E = 50°
∴Angles of ΔDEF
`∠`D = 70°, `∠`E = 50°, `∠`F = 60°
APPEARS IN
RELATED QUESTIONS
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
D, E, and F are the mid-points of the sides AB, BC, and CA respectively of ΔABC. AE meets DF at O. P and Q are the mid-points of OB and OC respectively. Prove that DPQF is a parallelogram.
In triangle ABC, the medians BP and CQ are produced up to points M and N respectively such that BP = PM and CQ = QN. Prove that:
- M, A, and N are collinear.
- A is the mid-point of MN.
In parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The line segments AF and BF meet the line segments ED and EC at points G and H respectively.
Prove that:
(i) Triangles HEB and FHC are congruent;
(ii) GEHF is a parallelogram.
D, E and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC. Prove that ΔDEF is also isosceles.
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: ∠EFG = 90°
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: The line drawn through G and parallel to FE and bisects DA.
In ΔABC, D and E are the midpoints of the sides AB and AC respectively. F is any point on the side BC. If DE intersects AF at P show that DP = PE.
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: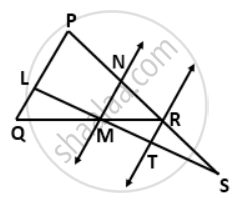
ST = `(1)/(3)"LS"`
D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral triangle ABC. Show that ∆DEF is also an equilateral triangle.
