Advertisements
Advertisements
Question
In parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The line segments AF and BF meet the line segments ED and EC at points G and H respectively.
Prove that:
(i) Triangles HEB and FHC are congruent;
(ii) GEHF is a parallelogram.
Solution
The figure is shown below
(i) From ΔHEB and ΔFHC
BE = FC
∠EHB = ∠FHC ...[ Opposite angle ]
∠HBE = ∠HFC
∴ ΔHEB ≅ ΔFHC
∴ EH = CH , BH = FH
(ii) Similarly AG = GF and EG = DG …..(1)
For triangle ECD,
F and H are the mid-point of CD and EC.
Therefore HF || DE and
HF = `[1]/[2]` DE ....(2)
From (1) and (2) we get,
HF = EG and HF || EG
Similarly, we can show that EH = GF and EH || GF
Therefore GEHF is a parallelogram.
APPEARS IN
RELATED QUESTIONS
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
ABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE = BF = CG = DH. Prove that EFGH is a square.
BM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If
L is the mid-point of BC, prove that LM = LN.
Fill in the blank to make the following statement correct
The triangle formed by joining the mid-points of the sides of an isosceles triangle is
In ∆ABC, E is the mid-point of the median AD, and BE produced meets side AC at point Q.
Show that BE: EQ = 3: 1.
In triangle ABC, P is the mid-point of side BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R.
Prove that : (i) AP = 2AR
(ii) BC = 4QR
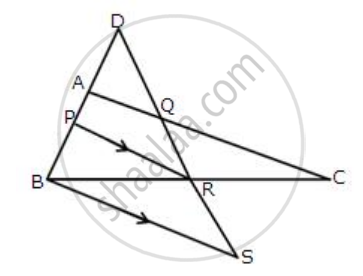
In the figure, give below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that:
(i) AQ // BS
(ii) DS = 3 Rs.
In triangle ABC, the medians BP and CQ are produced up to points M and N respectively such that BP = PM and CQ = QN. Prove that:
- M, A, and N are collinear.
- A is the mid-point of MN.
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: The line drawn through G and parallel to FE and bisects DA.
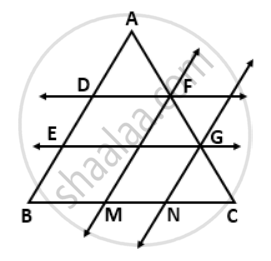
In AABC, D and E are two points on the side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet the side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meet the side BC at points M and N respectively. Prove that BM = MN = NC.