Advertisements
Advertisements
Question
In triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meets side BC at points M and N respectively. Prove that: BM = MN = NC.
Solution
The figure is shown below
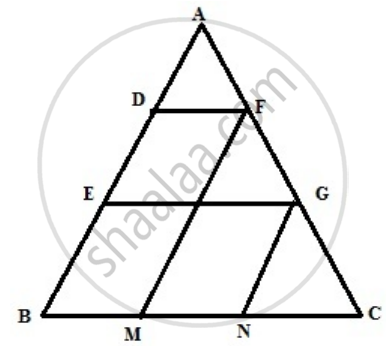
AD = DE = EB
In ΔAEG
AD = DE & DF || EG
Using mid point theorem
F is midpoint of AG
∴ AF = FG ...(1)
DF || EG || BC and DE = BE,
∴ FG = GC ...(2)
(1), (2) we get
AF = GF = GC
Similarly since GN || FM || AB
∴ BM = MN = NC
Hence, proved.
APPEARS IN
RELATED QUESTIONS
In a ΔABC, BM and CN are perpendiculars from B and C respectively on any line passing
through A. If L is the mid-point of BC, prove that ML = NL.
In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
A parallelogram ABCD has P the mid-point of Dc and Q a point of Ac such that
CQ = `[1]/[4]`AC. PQ produced meets BC at R.

Prove that
(i)R is the midpoint of BC
(ii) PR = `[1]/[2]` DB
In trapezium ABCD, AB is parallel to DC; P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E.
Prove that:
- Point P bisects BE,
- PQ is parallel to AB.
In triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
In the given figure, AD and CE are medians and DF // CE.
Prove that: FB = `1/4` AB.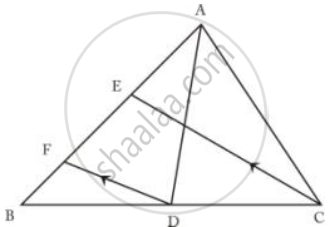
In parallelogram PQRS, L is mid-point of side SR and SN is drawn parallel to LQ which meets RQ produced at N and cuts side PQ at M. Prove that M is the mid-point of PQ.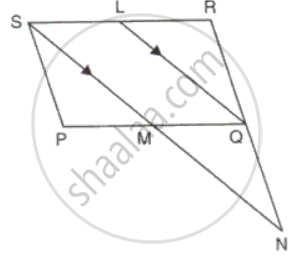
In ΔABC, D and E are the midpoints of the sides AB and BC respectively. F is any point on the side AC. Also, EF is parallel to AB. Prove that BFED is a parallelogram.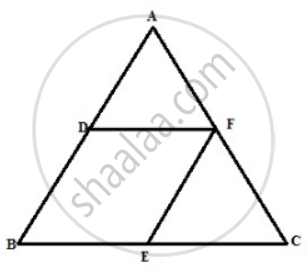
Remark: Figure is incorrect in Question
In ∆ABC, AB = 5 cm, BC = 8 cm and CA = 7 cm. If D and E are respectively the mid-points of AB and BC, determine the length of DE.
P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.
