Advertisements
Advertisements
Question
In a ΔABC, BM and CN are perpendiculars from B and C respectively on any line passing
through A. If L is the mid-point of BC, prove that ML = NL.
Solution
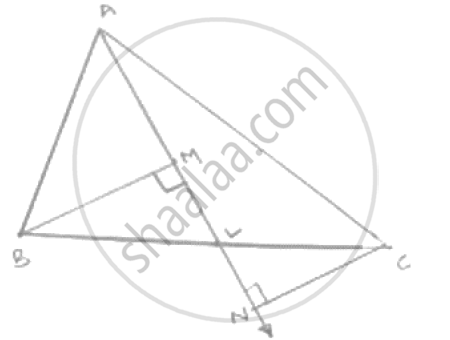
In B
Given that
In Δ BLM and Δ CLN
`∠`BML = `∠` CNL = 90°
BL = CL [L is the midpoint of BC]
`∠`MLB = `∠`NLC [vertically opposite angle]
∴ ΔBLM = ΔCLN ( A . L . A . S )
∴ LM = LN [Corresponding plats parts of congruent triangles]
APPEARS IN
RELATED QUESTIONS
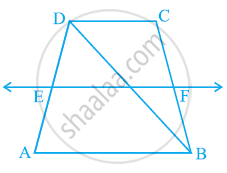
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
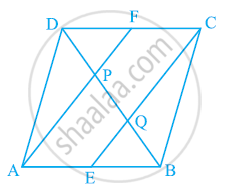
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see the given figure). Show that the line segments AF and EC trisect the diagonal BD.
In Fig. below, BE ⊥ AC. AD is any line from A to BC intersecting BE in H. P, Q and R are
respectively the mid-points of AH, AB and BC. Prove that ∠PQR = 90°.

In the given figure, `square`PQRS and `square`MNRL are rectangles. If point M is the midpoint of side PR then prove that,
- SL = LR
- LN = `1/2`SQ

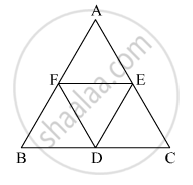
In the given figure, ΔABC is an equilateral traingle. Points F, D and E are midpoints of side AB, side BC, side AC respectively. Show that ΔFED is an equilateral traingle.
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P.
Prove that:
(i) BP = 2AD
(ii) O is the mid-point of AP.
In parallelogram PQRS, L is mid-point of side SR and SN is drawn parallel to LQ which meets RQ produced at N and cuts side PQ at M. Prove that M is the mid-point of PQ.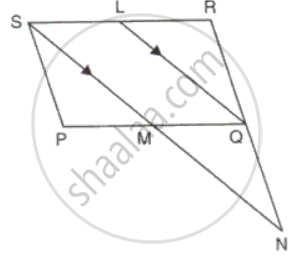
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: The line drawn through G and parallel to FE and bisects DA.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: EGFH is a parallelogram.
