Advertisements
Advertisements
Question
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: The line drawn through G and parallel to FE and bisects DA.
Solution
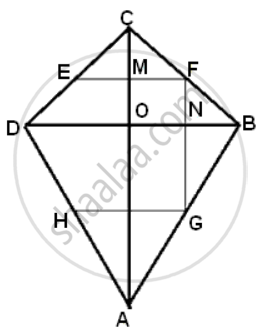
In ΔABD,
G is the mid-point of AB and HG || BD ...(from (ii) EF || DB and EF || HG)
Therefore, HG || DB
Therefore, H is the mid-point of DA.
Hence, the line drawn through G and parallel to FE bisects DA.
APPEARS IN
RELATED QUESTIONS
In a triangle ∠ABC, ∠A = 50°, ∠B = 60° and ∠C = 70°. Find the measures of the angles of
the triangle formed by joining the mid-points of the sides of this triangle.
In a ΔABC, BM and CN are perpendiculars from B and C respectively on any line passing
through A. If L is the mid-point of BC, prove that ML = NL.
BM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If
L is the mid-point of BC, prove that LM = LN.
D and F are midpoints of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
- Prove that BDFE is a parallelogram
- Find AB, if EF = 4.8 cm.
In triangle ABC ; D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F.
Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm,
find the perimeter of the parallelogram BDEF.
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find FE, if BC = 14 cm
In ΔABC, BE and CF are medians. P is a point on BE produced such that BE = EP and Q is a point on CF produced such that CF = FQ. Prove that: A is the mid-point of PQ.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
In ΔABC, P is the mid-point of BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that: AP = 2AR
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: ΔGEA ≅ ΔGFD
