Advertisements
Advertisements
Question
In triangle ABC ; D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F.
Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm,
find the perimeter of the parallelogram BDEF.
Solution
The figure is shown below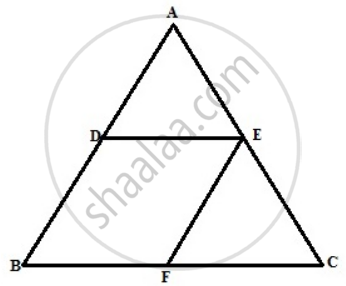
From figure since E is the midpoint of AC and EF || AB
Therefore F is the midpoint of BC and 2DE = BC or DE = BF
Again D and E are midpoints,
therefore DE || BF and EF = BD
Hence BDEF is a parallelogram.
Now,
BD = EF = `1/2"AB" = 1/2` x 16 = 8 cm
BF = DE = `1/2"BC" = 1/2` x 18 = 9 cm
Therefore perimeter of BDEF = 2( BF + EF ) = 2( 9 + 8 ) = 34 cm.
APPEARS IN
RELATED QUESTIONS
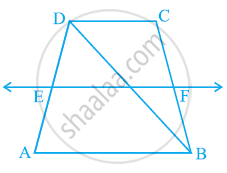
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
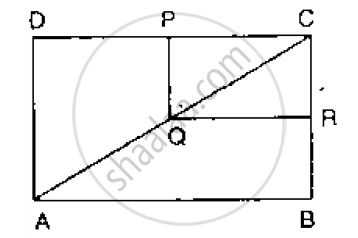
In the below Fig, ABCD and PQRC are rectangles and Q is the mid-point of Prove thaT
i) DP = PC (ii) PR = `1/2` AC
In the given figure, seg PD is a median of ΔPQR. Point T is the mid point of seg PD. Produced QT intersects PR at M. Show that `"PM"/"PR" = 1/3`.
[Hint: DN || QM]

In ΔABC, AB = 12 cm and AC = 9 cm. If M is the mid-point of AB and a straight line through M parallel to AC cuts BC in N, what is the length of MN?
If L and M are the mid-points of AB, and DC respectively of parallelogram ABCD. Prove that segment DL and BM trisect diagonal AC.
In parallelogram ABCD, P is the mid-point of DC. Q is a point on AC such that CQ = `(1)/(4)"AC"`. PQ produced meets BC at R. Prove that
(i) R is the mid-point of BC, and
(ii) PR = `(1)/(2)"DB"`.
In ΔABC, D and E are the midpoints of the sides AB and AC respectively. F is any point on the side BC. If DE intersects AF at P show that DP = PE.
In the given figure, T is the midpoint of QR. Side PR of ΔPQR is extended to S such that R divides PS in the ratio 2:1. TV and WR are drawn parallel to PQ. Prove that T divides SU in the ratio 2:1 and WR = `(1)/(4)"PQ"`.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if ______.
E and F are respectively the mid-points of the non-parallel sides AD and BC of a trapezium ABCD. Prove that EF || AB and EF = `1/2` (AB + CD).
[Hint: Join BE and produce it to meet CD produced at G.]
