Advertisements
Advertisements
प्रश्न
In triangle ABC ; D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F.
Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm,
find the perimeter of the parallelogram BDEF.
उत्तर
The figure is shown below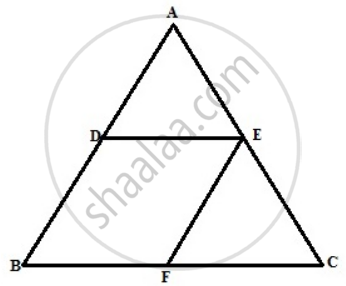
From figure since E is the midpoint of AC and EF || AB
Therefore F is the midpoint of BC and 2DE = BC or DE = BF
Again D and E are midpoints,
therefore DE || BF and EF = BD
Hence BDEF is a parallelogram.
Now,
BD = EF = `1/2"AB" = 1/2` x 16 = 8 cm
BF = DE = `1/2"BC" = 1/2` x 18 = 9 cm
Therefore perimeter of BDEF = 2( BF + EF ) = 2( 9 + 8 ) = 34 cm.
APPEARS IN
संबंधित प्रश्न
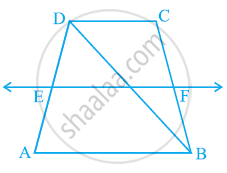
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
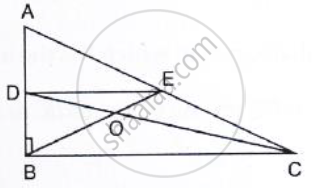
In a ΔABC, BM and CN are perpendiculars from B and C respectively on any line passing
through A. If L is the mid-point of BC, prove that ML = NL.
In Fig. below, triangle ABC is right-angled at B. Given that AB = 9 cm, AC = 15 cm and D,
E are the mid-points of the sides AB and AC respectively, calculate
(i) The length of BC (ii) The area of ΔADE.
ABC is a triang D is a point on AB such that AD = `1/4` AB and E is a point on AC such that AE = `1/4` AC. Prove that DE = `1/4` BC.
In the given figure, points X, Y, Z are the midpoints of side AB, side BC and side AC of ΔABC respectively. AB = 5 cm, AC = 9 cm and BC = 11 cm. Find the length of XY, YZ, XZ.

L and M are the mid-point of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
ABCD is a quadrilateral in which AD = BC. E, F, G and H are the mid-points of AB, BD, CD and Ac respectively. Prove that EFGH is a rhombus.

In a right-angled triangle ABC. ∠ABC = 90° and D is the midpoint of AC. Prove that BD = `(1)/(2)"AC"`.
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square is also a square.
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: The line drawn through G and parallel to FE and bisects DA.
