Advertisements
Advertisements
प्रश्न
In the given figure, points X, Y, Z are the midpoints of side AB, side BC and side AC of ΔABC respectively. AB = 5 cm, AC = 9 cm and BC = 11 cm. Find the length of XY, YZ, XZ.

उत्तर
AB = 5 cm, AC = 9 cm and BC = 11 cm …(Given)
In ∆ABC,
Points X and Y are the midpoints of sides AB and BC respectively. ...(Given)
∴ XY = `1/2` AC ...(From midpoint theorem)
∴ XY = `1/2xx 9`
∴ XY = 4.5 cm
In ∆ABC,
Points Y and Z are the midpoints of sides BC and AC respectively. ...(Given)
∴ YZ = `1/2` AB ...(From midpoint theorem)
∴ YZ = `1/2xx 5`
∴ YZ = 2.5 cm
In ∆ABC,
Points X and Z are the midpoints of lines AB and AC respectively. ...(Given)
∴ XZ = `1/2` BC ...(From midpoint theorem)
∴ XZ = `1/2xx 11`
∴ XZ = 5.5 cm
APPEARS IN
संबंधित प्रश्न
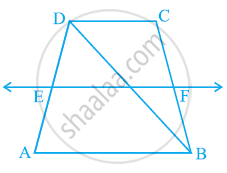
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
ABCD is a kite having AB = AD and BC = CD. Prove that the figure formed by joining the
mid-points of the sides, in order, is a rectangle.
In the given figure, `square`PQRS and `square`MNRL are rectangles. If point M is the midpoint of side PR then prove that,
- SL = LR
- LN = `1/2`SQ

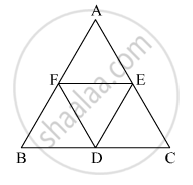
In the given figure, ΔABC is an equilateral traingle. Points F, D and E are midpoints of side AB, side BC, side AC respectively. Show that ΔFED is an equilateral traingle.
In ΔABC, D is the mid-point of AB and E is the mid-point of BC.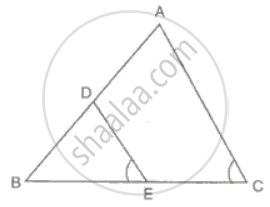
Calculate:
(i) DE, if AC = 8.6 cm
(ii) ∠DEB, if ∠ACB = 72°
In a parallelogram ABCD, M is the mid-point AC. X and Y are the points on AB and DC respectively such that AX = CY. Prove that:
(i) Triangle AXM is congruent to triangle CYM, and
(ii) XMY is a straight line.
AD is a median of side BC of ABC. E is the midpoint of AD. BE is joined and produced to meet AC at F. Prove that AF: AC = 1 : 3.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: ΔGEA ≅ ΔGFD
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: A is the mid-point of PQ.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rhombus, if ______.
