Advertisements
Advertisements
प्रश्न
In the given figure, `square`PQRS and `square`MNRL are rectangles. If point M is the midpoint of side PR then prove that,
- SL = LR
- LN = `1/2`SQ

उत्तर
(i) `square`LMNR and `square`MNRL are rectangles.
∴ Side LM || Side RN ...(Opposite sides of rectangle)
That is, Side LM || Side RQ ...(R-N-Q) ...(i)
Side RQ || Side SP ...(Opposite sides of the rectangle) ...(ii)
From (i) and (ii),
Side LM || Side SP ...(iii)
In ΔRSP,
Point M is the midpoint of Seg PR.
Line LM || Line SP ...[From (iii)]
∴ Point L is the midpoint of Seg SR. ...(Converse of Midpoint Theorem) ...(iv)
∴ SL = LR
(ii) The diagonals of a rectangle are congruent.
∴ SQ = PR ...(v)
LN = MR ...(vi)
Now, MR = `1/2` PR ...(Point M is the midpoint of line PR.) ...(vii)
∴ LN = `1/2` PR ...[From (vi) and (vii)] ...(viii)
∴ LN = `1/2` SQ ...[From (vii) and (viii)]
APPEARS IN
संबंधित प्रश्न
Let Abc Be an Isosceles Triangle in Which Ab = Ac. If D, E, F Be the Mid-points of the Sides Bc, Ca and a B Respectively, Show that the Segment Ad and Ef Bisect Each Other at Right Angles.
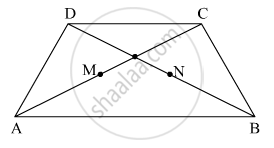
In the adjacent figure, `square`ABCD is a trapezium AB || DC. Points M and N are midpoints of diagonal AC and DB respectively then prove that MN || AB.
In the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF.
Show that: EF = AC.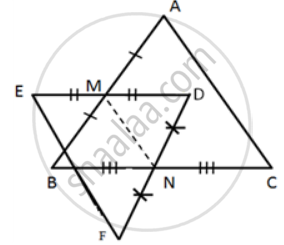
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P.
Prove that:
(i) BP = 2AD
(ii) O is the mid-point of AP.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: PQ, if AB = 12 cm and DC = 10 cm.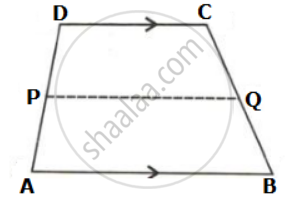
AD is a median of side BC of ABC. E is the midpoint of AD. BE is joined and produced to meet AC at F. Prove that AF: AC = 1 : 3.
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: The line drawn through G and parallel to FE and bisects DA.
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
If AE and DF intersect at G, and M and N are the midpoints of GB and GC respectively, prove that DMNF is a parallelogram.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if ______.
D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral triangle ABC. Show that ∆DEF is also an equilateral triangle.
